In queue using a stack problem, we have to implement the following functions of a queue using the standard functions of stack data structure,
- Enqueue: Add an element to the end of the queue
- Dequeue: Remove an element from the start of the queue
Table of Contents
Example
Input:
Enqueue(5)
Enqueue(11)
Enqueue(39)
Dequeue() // Returns 5
Enqueue(12)
Dequeue() // Returns 11
Dequeue() // Returns 39
Output:
5
11
39
Algorithm
A queue can be implemented using two stacks, there are two ways to implement a queue using stacks, first by making enqueue operation costly and second by making dequeue operation costly.
Method 1 (Costly Enqueue Operation) for Queue using Stacks
Create two stack st1 and st2. Visualize the queue in st1, the top of st1 is front of the queue, and moving downwards in st1 is similar to moving ahead in the queue.
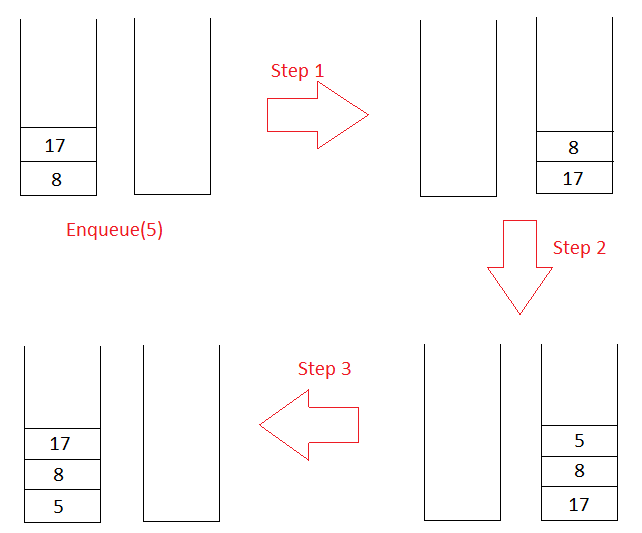
Enqueue(x)
Pushing x to the rear of the queue is the same as pushing x to the bottom of stack st1.
- Remove all the elements from st1 and push them to st2.
- Push x to st2.
- Remove all the elements from st2 and push them back to st1.
Time Complexity = O(n)A
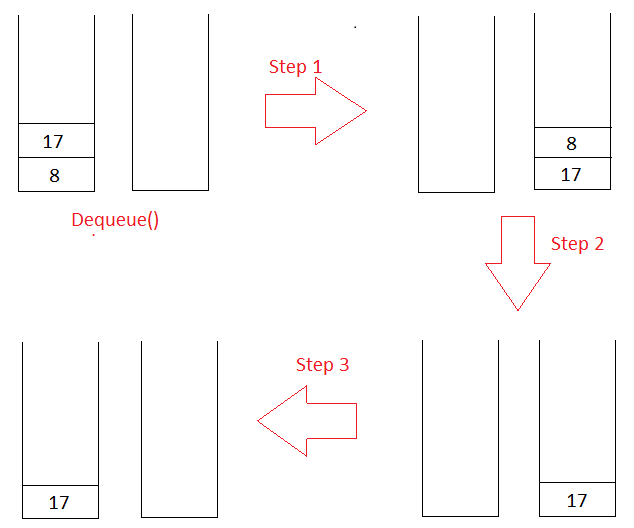
Dequeue()
Removing an element from the front of the queue is similar to removing the top of stack st1. So if st1 is not empty pop the top of st1 and return.
Time Complexity= O(1)
Overall Space Complexity of Method 1 = O(n)
JAVA Code for Queue using Stacks
import java.util.Stack;
public class QueueUsingStacks {
// Costly Enqueue Operation
private static Stack<Integer> st1;
private static Stack<Integer> st2;
private static void enqueue(int x) {
// remove all the elements from st1 and push them to st2
while (!st1.isEmpty()) {
st2.push(st1.pop());
}
// push x to st2
st2.push(x);
// remove all the elements from st2 and push them back to st1
while (!st2.isEmpty()) {
st1.push(st2.pop());
}
}
private static int dequeue() {
if (st1.isEmpty()) {
return -1;
}
// if st1 is not empty return and remove the top of st1
return st1.pop();
}
public static void main(String[] args) {
st1 = new Stack<>();
st2 = new Stack<>();
// Example
enqueue(5);
enqueue(11);
enqueue(39);
System.out.println(dequeue());
enqueue(12);
System.out.println(dequeue());
System.out.println(dequeue());
}
}5 11 39
C++ Code
#include<bits/stdc++.h>
using namespace std;
// Costly Enqueue Operation
stack<int> st1;
stack<int> st2;
void enqueue(int x) {
// remove all the elements from st1 and push them to st2
while (!st1.empty()) {
int curr = st1.top();
st1.pop();
st2.push(curr);
}
// push x to st2
st2.push(x);
// remove all the elements from st2 and push them back to st1
while (!st2.empty()) {
int curr = st2.top();
st2.pop();
st1.push(curr);
}
}
int dequeue() {
if (st1.empty()) {
return -1;
}
// if st1 is not empty return and remove the top of st1
int top = st1.top();
st1.pop();
return top;
}
int main() {
// Example
enqueue(5);
enqueue(11);
enqueue(39);
cout<<dequeue()<<endl;
enqueue(12);
cout<<dequeue()<<endl;
cout<<dequeue()<<endl;
return 0;
}5 11 39
Method 2 (Costly Dequeue Operation) for Queue using Stacks
Create two stacks st1 and st2. Visualize queue in st1, the top of st1 represents the rear of the queue, moving upwards in st1 is similar to moving ahead in the queue.
Enqueue(x)
Pushing x to the rear of the queue is similar to pushing x to the top of stack_st1. So push x to top of st1.
Time Complexity= O(1)
Dequeue()
Removing an element from the front of the queue is similar to removing an element from the bottom of stack_st1. So, if st1 is not empty,
- Remove all the elements from st1 and push them to st2.
- Pop the top of st2 and store it in a variable top.
- Remove all the elements from st2 and push them back to st1.
- Return top
Time Complexity= O(n)
Overall Space Complexity of Method 2 = O(n)
JAVA Code
import java.util.Stack;
public class QueueUsingStacks {
// Costly Dequeue Operation
private static Stack<Integer> st1;
private static Stack<Integer> st2;
private static void enqueue(int x) {
// push x to top of st1
st1.push(x);
}
private static int dequeue() {
if (st1.isEmpty()) {
return -1;
}
// if st1 is not empty
// remove all the elements from st1 and push them to st2
while (!st1.isEmpty()) {
st2.push(st1.pop());
}
// pop the top of st2 and store it in a variable top
int top = st2.pop();
// remove all the elements from st2 and push them back to st1
while (!st2.isEmpty()) {
st1.push(st2.pop());
}
// return top
return top;
}
public static void main(String[] args) {
st1 = new Stack<>();
st2 = new Stack<>();
// Example
enqueue(5);
enqueue(11);
enqueue(39);
System.out.println(dequeue());
enqueue(12);
System.out.println(dequeue());
System.out.println(dequeue());
}
}5 11 39
C++ Code
#include<bits/stdc++.h>
using namespace std;
// Costly Dequeue Operation
stack<int> st1;
stack<int> st2;
void enqueue(int x) {
// push x to top of st1
st1.push(x);
}
int dequeue() {
if (st1.empty()) {
return -1;
}
// if st1 is not empty
// remove all the elements from st1 and push them to st2
while (!st1.empty()) {
int curr = st1.top();
st1.pop();
st2.push(curr);
}
// pop the top of st2 and store it in a variable top
int top = st2.top();
st2.pop();
// remove all the elements from st2 and push them back to st1
while (!st2.empty()) {
int curr = st2.top();
st2.pop();
st1.push(curr);
}
// return top
return top;
}
int main() {
// Example
enqueue(5);
enqueue(11);
enqueue(39);
cout<<dequeue()<<endl;
enqueue(12);
cout<<dequeue()<<endl;
cout<<dequeue()<<endl;
return 0;
}5 11 39