Table of Contents
Problem Statement
The problem “Find Maximum Level sum in Binary Tree” states that you are given a binary tree with positive and negative nodes, find the maximum sum of a level in the binary tree.
Example
Input
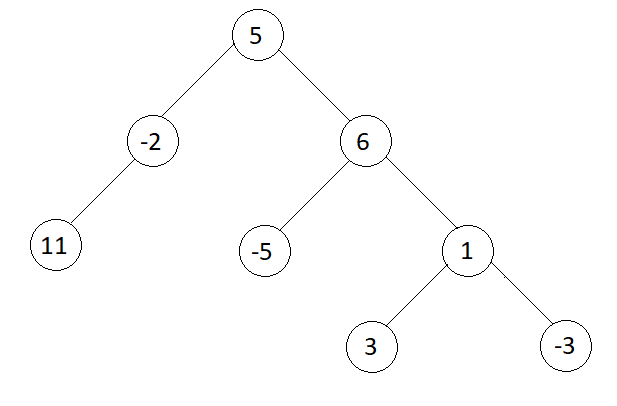
7
Explanation
First Level : Sum = 5
Second Level : Sum = (-2 + 6) = 4
Third Level : Sum = (11 + (-5) + 1) = 7
Fourth Level : Sum = (3 + (-3)) = 0
Max Sum = 7
Algorithm to Find Maximum Level sum in Binary Tree
The idea is to do a level order traversal and for each level calculate the sum of all the nodes of that level. If the sum is greater than maximum sum, update the maximum sum.
- Create a queue, and push the root node to the queue. Initialize a variable maxSum as negative infinity.
- While the queue is not empty repeat step 3 and 4.
- At this moment one level is present in the queue. Initialize a variable named size as the size of queue and a variable sum as 0.
- Run a loop from i = 0 to size, and at each iteration pop out an element from the queue. Add the value of this element to variable sum and push the children of popped out node to the queue. At the end of the loop if sum is greater than maxSum, update maxSum as sum.
- Return maxSum.
Explanation
Consider the tree in the example above
Step 1
Create a queue and push root to it. Initialize a variable maxSum as negative infinity.
queue = 5 and maxSum = -infinity
Step 2
Repeat Step 3 and 4, while queue is not empty.
Step 3 and 4
Iteration 1
size = 1, sum = 0
Remove all the elements from queue, add the value of each element to sum, and push the children of every element to the queue.
sum = 5, queue = -2 -> 6
Update maxSum, so, maxSum = 5
Iteration 2
size = 2, sum = 0
Remove all the elements from queue, add the value of each element to sum, and push the children of every element to the queue.
sum = (-2 + 6) = 4, queue = 11 -> -5 -> 1
Update maxSum, so, maxSum = 5
Iteration 3
size = 3, sum = 0
Remove all the elements from queue, add the value of each element to sum, and push the children of every element to the queue.
sum = (11 + (-5) + 1) = 7, queue = 3 -> -3
Update maxSum, so, maxSum = 7
Iteration 4
size = 2, sum = 0
Remove all the elements from queue, add the value of each element to sum, and push the children of every element to the queue.
sum = (3 + (-3)) = 0, queue = null
Update maxSum, so, maxSum = 7
As the queue becomes empty so we stop and the max sum of a level is 7.
Code
Java Code to Find Maximum Level sum in Binary Tree
import java.util.LinkedList;
import java.util.Queue;
class FindMaximumLevelSumInBinaryTree {
// class representing node of binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
private static int maxLevelSum(Node root) {
if (root == null) {
return Integer.MIN_VALUE;
}
// create a queue and push root to it
Queue<Node> queue = new LinkedList<>();
queue.add(root);
// initialize maxSum as negative infinity
int maxSum = Integer.MIN_VALUE;
// while queue is not empty
while (!queue.isEmpty()) {
// At this moment the queue contains one level in it
// initialize size as size of queue
int size = queue.size();
// initialize sum as 0, this represents the sum of a level
int sum = 0;
// run a loop from 0 to size
for (int i = 0; i < size; i++) {
// remove an element from queue
Node curr = queue.poll();
// add the value of current element to sum
sum += curr.data;
// push the children of current element to queue
if (curr.left != null)
queue.add(curr.left);
if (curr.right != null)
queue.add(curr.right);
}
// update max sum
maxSum = Math.max(maxSum, sum);
}
// return max sum
return maxSum;
}
public static void main(String[] args) {
// Example tree
Node root = new Node(5);
root.left = new Node(-2);
root.right = new Node(6);
root.left.left = new Node(11);
root.right.left = new Node(-5);
root.right.right = new Node(1);
root.right.right.left = new Node(3);
root.right.right.right = new Node(-3);
System.out.println(maxLevelSum(root));
}
}7
C++ Code to Find Maximum Level sum in Binary Tree
#include <bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to create a new node with data d
Node* newNode(int d) {
Node *node = new Node(d);
return node;
}
int maxLevelSum(Node *root) {
if (root == NULL) {
return INT_MIN;
}
// create a queue and push root to it
queue<Node*> q;
q.push(root);
// initialize maxSum as negative infinity
int maxSum = INT_MIN;
// while queue is not empty
while (!q.empty()) {
// At this moment the queue contains one level in it
// initialize size as size of queue
int size = q.size();
// initialize sum as 0, this represents the sum of a level
int sum = 0;
// run a loop from 0 to size
for (int i = 0; i < size; i++) {
// remove an element from queue
Node *curr = q.front();
q.pop();
// add the value of current element to sum
sum += curr->data;
// push the children of current element to queue
if (curr->left != NULL)
q.push(curr->left);
if (curr->right != NULL)
q.push(curr->right);
}
// update max sum
maxSum = std::max(maxSum, sum);
}
// return max sum
return maxSum;
}
int main() {
// Example tree
Node *root = newNode(5);
root->left = newNode(-2);
root->right = newNode(6);
root->left->left = newNode(11);
root->right->left = newNode(-5);
root->right->right = newNode(1);
root->right->right->left = newNode(3);
root->right->right->right = newNode(-3);
cout<<maxLevelSum(root)<<endl;
return 0;
}7
Complexity Analysis
Time Complexity
O(N), because we simply traversed over all the tree elements and pushed them twice in the queue. So the time complexity is linear.
Space Complexity
O(N), because we used queue to store the elements of each level. The space complexity is also linear.