Table of Contents
Problem Statement
The problem “Check if all levels of two Binary Tree are anagrams or not” says that you are given two Binary Trees, check if all the levels of the two trees are anagrams or not.
Examples
Input
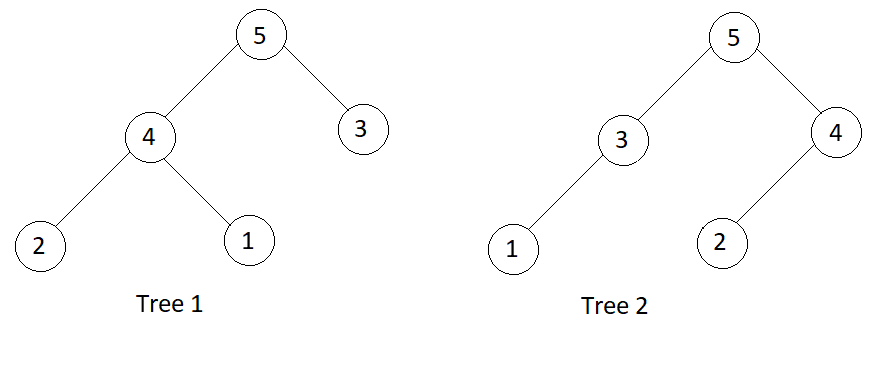
true
Input
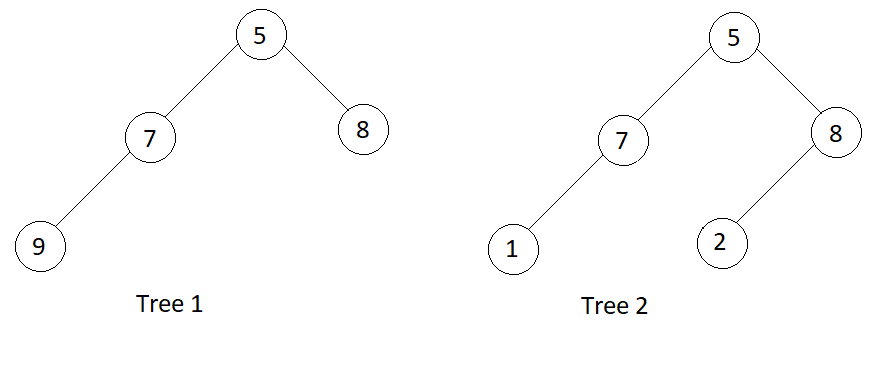
false
Algorithm to Check if all levels of two Binary Tree are anagrams or not
We will use hashing for solving this problem. Traverse every level of two trees simultaneously. For the first tree, store the element and frequency of current level in a HashMap and for the second tree’s current level, if the current element is not present in HashMap. All the levels are not anagrams. Else reduce the frequency of that element in the HashMap. If at the end of traversal, the HashMap is empty, this level of both trees is anagram continue for next levels, otherwise all levels are not anagrams.
- Create two queues q1 and q2, q1 is used to traverse tree 1 and q2 is used to traverse q2.
- Push the root of tree 1 to q1 and root of tree 2 to q2.
- While either q1 is not empty or q2 is not empty repeat step 4, 5 and 6.
- Create a HashMap to store elements and frequency of current level elements. Initialize an integer size1 as size of q1. Run a loop from 0 to less than size1. At every iteration pop out an element from the queue q1 and add it to the HashMap. Push the children of current element into the queue.
- Initialize an integer size2 as size of q2. Run a loop from 0 to less than size2. At every iteration, pop out an element from the queue q2 and if this element is present in HashMap reduce its frequency by 1, else return false immediately.
- If at the end of loop, HashMap contains an element, return false, else this level of the two trees are anagrams, continue for the next level.
- If we reach here, all the levels of the two trees are anagrams, so return true.
Code
Java code to Check if all levels of two Binary Tree are anagrams or not
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Queue;
class CheckIfAllLevelsOfTwoBinaryTreeAreAnagramsOrNot {
// class representing node of a binary tree
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
private static boolean checkIsAnagrams(Node tree1, Node tree2) {
// create two queues
Queue<Node> q1 = new LinkedList<>();
Queue<Node> q2 = new LinkedList<>();
// add root of tree1 to q1
q1.add(tree1);
// add root of tree2 to q2
q2.add(tree2);
// while either of q1 or q2 is not empty
while (!q1.isEmpty() || !q2.isEmpty()) {
// create a hash map to store freq of elements of a level
HashMap<Integer, Integer> freq = new HashMap<>();
// traverse this level of tree1
int size1 = q1.size();
for (int i = 0; i < size1; i++) {
// remove a node from queue
Node curr = q1.poll();
// add the element to hash map
if (freq.containsKey(curr.data)) {
freq.put(curr.data, freq.get(curr.data) + 1);
} else {
freq.put(curr.data, 1);
}
// add curr's children to queue
if (curr.left != null)
q1.add(curr.left);
if (curr.right != null)
q1.add(curr.right);
}
// traverse this level of tree2
int size2 = q2.size();
for (int i = 0; i < size2; i++) {
// remove a node from q2
Node curr = q2.poll();
// decrease the frequency of this element in hash map
if (freq.containsKey(curr.data)) {
int frequency = freq.get(curr.data);
frequency--;
if (frequency == 0) {
freq.remove(curr.data);
} else {
freq.put(curr.data, frequency);
}
} else {
return false;
}
// add curr's children to queue
if (curr.left != null)
q2.add(curr.left);
if (curr.right != null)
q2.add(curr.right);
}
// if there is an element in the hash map
// the two tree's current levels are not anagrams
if (freq.size() > 0) {
return false;
}
}
// all the levels are anagrams, return true
return true;
}
public static void main(String[] args) {
// Example 1
Node tree1_1 = new Node(5);
tree1_1.left = new Node(4);
tree1_1.right = new Node(3);
tree1_1.left.left = new Node(2);
tree1_1.left.right = new Node(1);
Node tree2_1 = new Node(5);
tree2_1.left = new Node(3);
tree2_1.right = new Node(4);
tree2_1.left.left = new Node(1);
tree2_1.right.left = new Node(2);
System.out.println(checkIsAnagrams(tree1_1, tree2_1));
// Example 2
Node tree1_2 = new Node(5);
tree1_2.left = new Node(7);
tree1_2.right = new Node(8);
tree1_2.left.left = new Node(9);
Node tree2_2 = new Node(5);
tree2_2.left = new Node(7);
tree2_2.right = new Node(8);
tree2_2.left.left = new Node(1);
tree2_2.right.left = new Node(2);
System.out.println(checkIsAnagrams(tree1_2, tree2_2));
}
}true false
C++ Code to Check if all levels of two Binary Tree are anagrams or not
#include<bits/stdc++.h>
using namespace std;
// class representing node of a binary tree
class Node {
public:
int data;
Node *left;
Node *right;
Node(int d) {
data = d;
left = right = NULL;
}
};
// function to create a new node with given data
Node* newNode(int data) {
Node *node = new Node(data);
return node;
}
bool checkIsAnagrams(Node *tree1, Node *tree2) {
// create two queues
queue<Node *> q1;
queue<Node *> q2;
// add root of tree1 to q1
q1.push(tree1);
// add root of tree2 to q2
q2.push(tree2);
// while either of q1 or q2 is not empty
while (!q1.empty() || !q2.empty()) {
// create a hash map to store freq of elements of a level
unordered_map<int, int> freq;
// traverse this level of tree1
int size1 = q1.size();
for (int i = 0; i < size1; i++) {
// remove a node from queue
Node *curr = q1.front();
q1.pop();
// add the element to hash map
auto itr = freq.find(curr->data);
if (itr != freq.end()) {
itr->second++;
} else {
freq.insert(make_pair(curr->data, 1));
}
// add curr's children to queue
if (curr->left != NULL)
q1.push(curr->left);
if (curr->right != NULL)
q1.push(curr->right);
}
// traverse this level of tree2
int size2 = q2.size();
for (int i = 0; i < size2; i++) {
// remove a node from q2
Node *curr = q2.front();
q2.pop();
// decrease the frequency of this element in hash map
auto itr = freq.find(curr->data);
if (itr != freq.end()) {
itr->second--;
if (itr->second == 0) {
freq.erase(itr);
}
} else {
return false;
}
// add curr's children to queue
if (curr->left != NULL)
q2.push(curr->left);
if (curr->right != NULL)
q2.push(curr->right);
}
// if there is an element in the hash map
// the two tree's current levels are not anagrams
if (freq.size() != 0)
return false;
}
// all the levels are anagrams, return true
return true;
}
int main() {
// Example 1
Node *tree1_1 = newNode(5);
tree1_1->left = newNode(4);
tree1_1->right = newNode(3);
tree1_1->left->left = newNode(2);
tree1_1->left->right = newNode(1);
Node *tree2_1 = new Node(5);
tree2_1->left = newNode(3);
tree2_1->right = newNode(4);
tree2_1->left->left = newNode(1);
tree2_1->right->left = newNode(2);
if (checkIsAnagrams(tree1_1, tree2_1)) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 2
Node *tree1_2 = newNode(5);
tree1_2->left = newNode(7);
tree1_2->right = newNode(8);
tree1_2->left->left = newNode(9);
Node *tree2_2 = newNode(5);
tree2_2->left = newNode(7);
tree2_2->right = newNode(8);
tree2_2->left->left = newNode(1);
tree2_2->right->left = newNode(2);
if (checkIsAnagrams(tree1_2, tree2_2)) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}true false
Complexity Analysis
As we traversed both the trees exactly once and used two queues for level order traversal, so
Time Complexity = O(n + m)
Space Complexity = O(n + m)
where n is the number of nodes in tree 1 and m is the number of nodes in tree 2.