Table of Contents
Problem Statement
The problem “Find the largest multiple of 3” states that you are given an array of positive integers(0 to 9). Find the maximum multiple of 3 that can be formed by rearranging the elements of the array.
Examples
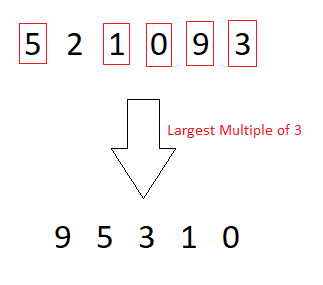
arr[] = {5, 2, 1, 0, 9, 3}9 5 3 1 0
arr[] = {1, 2, 3, 4, 5}5 4 3 2 1
Algorithm to Find the largest multiple of 3
Every multiple of three has a special property. he sum of its digits are also divisible by 3, for example,
123 is divisible by 3, so (1 + 2 + 3) = 6 is also divisible by 3. So, this property can be used to solve the above problem.
Sort the array in ascending order and maintain three queues, queue0 to store all the elements in the array that leave remainder 0 when divided by 3, queue1 to store all the elements in the array that leave remainder 1 when divided by 3 and queue2 to store the elements in the array that leave remainder 2 when divided by 3.
According to the sum of all the elements in the array, there are 3 cases, that is,
Case 1 : divisible by 3
Store all the elements of the three queues in an array and sort the array in descending order, this is the answer.
Case 2 : Leaves remainder 1 when divided by 3
Remove 1 element from queue1 or if queue1 is empty remove 2 elements from queue2, if it is not possible to do any of these there is no way to form a multiple of 3.
Move all the elements remaining in the queues to an array and sort the array in descending order, this is the answer.
Case 3 : Leaves remainder 2 when divided by 3
Remove 1 element from queue2 or if queue2 is empty remove 2 elements from queue1 or if it is not possible to do any of these there is no way to from a multiple if 3.
Move all the elements remaining in the queues to an array, sort the array in descending order, this is the answer.
Code
Java Code to Find the largest multiple of 3
import java.util.*;
class FindTheLargestMultipleOf3 {
private static void fillAns(ArrayList<Integer> ans, Queue<Integer> q0, Queue<Integer> q1, Queue<Integer> q2) {
while (!q0.isEmpty()) {
ans.add(q0.poll());
}
while (!q1.isEmpty()) {
ans.add(q1.poll());
}
while (!q2.isEmpty()) {
ans.add(q2.poll());
}
}
private static boolean findLargestMultiple(int[] arr) {
int n = arr.length;
// sort the array in ascending order
Arrays.sort(arr);
// maintain 3 queues as mentioned
Queue<Integer> queue0 = new LinkedList<>();
Queue<Integer> queue1 = new LinkedList<>();
Queue<Integer> queue2 = new LinkedList<>();
// variable to store the sum of all the elements in array
int sum = 0;
// traverse the array and add elements to queue
// also find the sum
for (int i = 0; i < n; i++) {
sum += arr[i];
if (arr[i] % 3 == 0) {
queue0.add(arr[i]);
} else if (arr[i] % 3 == 1) {
queue1.add((arr[i]));
} else {
queue2.add(arr[i]);
}
}
// if sum is divisible by 3, do nothing
if (sum % 3 == 0) {
}
// if sum leaves remainder 1 when divided by 3
else if (sum % 3 == 1) {
// remove 1 element from queue1
if (!queue1.isEmpty()) {
queue1.remove();
} else {
// or remove two elements from queue2
if (!queue2.isEmpty()) {
queue2.remove();
} else {
return false;
}
if (!queue2.isEmpty()) {
queue2.remove();
} else {
return false;
}
}
}
// if sum leaves remainder 2 when divided by 3
else {
// remove one element from queue2
if (!queue2.isEmpty()) {
queue2.remove();
} else {
// or remove 2 elements from queue1
if (!queue1.isEmpty()) {
queue1.remove();
} else {
return false;
}
if (!queue1.isEmpty()) {
queue1.remove();
} else {
return false;
}
}
}
// add the remaining elements to a list
ArrayList<Integer> ans = new ArrayList<>();
fillAns(ans, queue0, queue1, queue2);
// sort the list in descending order, this is the answer
Collections.sort(ans, Collections.reverseOrder());
for (int i = 0; i < ans.size(); i++) {
System.out.print(ans.get(i) + " ");
}
System.out.println();
return true;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{5, 2, 1, 0, 9, 3};
if (!findLargestMultiple(arr1)) {
System.out.println("Not Possible");
}
// Example 2
int arr2[] = new int[]{1, 2, 3, 4, 5};
if (!findLargestMultiple(arr2)) {
System.out.println("Not Possible");
}
}
}9 5 3 1 0 5 4 3 2 1
C++ Code to Find the largest multiple of 3
#include <bits/stdc++.h>
using namespace std;
void fillAns(vector<int> &ans, queue<int> q0, queue<int> q1, queue<int> q2) {
while (!q0.empty()) {
ans.push_back(q0.front());
q0.pop();
}
while (!q1.empty()) {
ans.push_back(q1.front());
q1.pop();
}
while (!q2.empty()) {
ans.push_back(q2.front());
q2.pop();
}
}
bool findLargestMultiple(int *arr, int n) {
// sort the array in ascending order
sort(arr, arr + n);
// maintain 3 queues as mentioned
queue<int> q0;
queue<int> q1;
queue<int> q2;
// variable to store the sum of all the elements in array
int sum = 0;
// traverse the array and add elements to queue
// also find the sum
for (int i = 0; i < n; i++) {
sum += arr[i];
if (arr[i] % 3 == 0) {
q0.push(arr[i]);
} else if (arr[i] % 3 == 1) {
q1.push(arr[i]);
} else {
q2.push(arr[i]);
}
}
// if sum is divisible by 3, do nothing
if (sum % 3 == 0) {
}
// if sum leaves remainder 1 when divided by 3
else if (sum % 3 == 1) {
// remove 1 element from queue1
if (!q1.empty()) {
q1.pop();
} else {
// or remove two elements from queue2
if (!q2.empty()) {
q2.pop();
} else {
return false;
}
if (!q2.empty()) {
q2.pop();
} else {
return false;
}
}
}
// if sum leaves remainder 2 when divided by 3
else {
// remove one element from queue2
if (!q2.empty()) {
q2.pop();
} else {
// or remove 2 elements from queue1
if (!q1.empty()) {
q1.pop();
} else {
return false;
}
if (!q1.empty()) {
q1.pop();
} else {
return false;
}
}
}
// add the remaining elements to a list
vector<int> ans;
fillAns(ans, q0, q1, q2);
// sort the list in descending order, this is the answer
sort(ans.begin(), ans.end(), greater<int>());
for (int i = 0; i < ans.size(); i++) {
cout<<ans[i]<<" ";
}
cout<<endl;
return true;
}
int main() {
// Example 1
int arr1[] = {5, 2, 1, 0, 9, 3};
if (!findLargestMultiple(arr1,sizeof(arr1) / sizeof(arr1[0]))) {
cout<<"Not Possible"<<endl;
}
// Example 2
int arr2[] = {1, 2, 3, 4, 5};
if (!findLargestMultiple(arr2,sizeof(arr2) / sizeof(arr2[0]))) {
cout<<"Not Possible"<<endl;
}
return 0;
}9 5 3 1 0 5 4 3 2 1
Complexity Analysis
Time Complexity
O(N log N), because we have been sorting the three intermediate queues. And in the worst case, all n elements may end up in a single queue. Then the worst case complexity will be O(N log N).
Space Complexity
O(N), as we have used the queues to store the N elements. The algorithm has linear space complexity.