Table of Contents
Problem Statement
Find the maximum sum rectangle in a 2D matrix i.e. to find a sub-matrix with maximum sum. A sub-matrix is nothing but a 2D array inside of the given 2D array. So, you have a matrix of signed integers, you need to calculate the sum of sub-matrices and find the maximum value.
Example
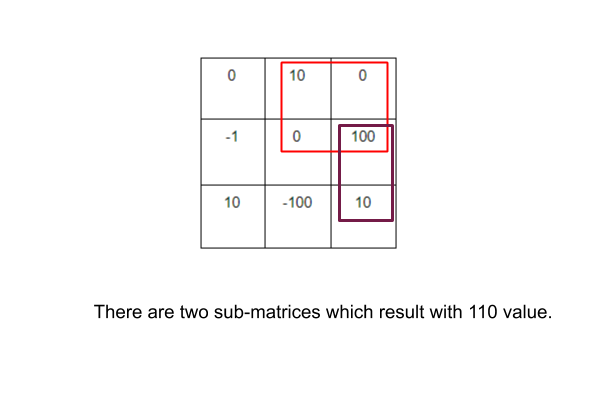
{ 0 10 0
-1 0 100
10 -100 10 }
110
Explanation: Here, in this given input we have two possible answers. Like if we choose a sub-matrix of size 2×2 from first row first column to second-row third column. And we can also select a sub-matrix of size 2×1 from the second-row third column to the third row, third column. Both of the results will give the same sum 110 as the answer.
{ 100
-10
100 }190
Explanation: Here, in this given input 2D array. We can choose the whole matrix as a result because that will provide us with a total of 190.
Approach for finding maximum sum rectangle in a 2D matrix
Naive Solution
We can find the maximum sum submatrix in given matrix by using a naive solution. We can use four nested loops each for different indices. So, one will be for starting row index, starting column index, ending row index, and ending column index. We can use a 2D prefix array for storing the sum of prefixes. This approach can optimize our naive approach a bit but that will not efficient enough though.
Efficient Solution
So, instead of using a naive solution, we will use Kadane’s algorithm for solving this problem efficiently. But the problem is now, how can we apply Kadane’s algorithm in a 2D matrix? We will promptly fix two columns, one for the left column and one for the right column. Then we store the sum between two columns in an array and then use Kadane’s algorithm for finding the maximum continuous sum of rows between those columns. We update our answer with the maximum value. After doing this for all possible combinations, we have our maximum sum rectangle in a 2D matrix.
Code to find the maximum sum rectangle in a 2D matrix
C++ Code
#include<bits/stdc++.h>
using namespace std;
int findMaximumSubMatrix(vector<vector<int>> matrix, int n, int m){
// stores the prefixSum of rows
vector<vector<int>> prefixSum(n,vector<int>(m));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
prefixSum[i][j] = matrix[i][j];
}
// calculation prefix sum for each row
for(int i=0;i<n;i++){
for(int j=1;j<m;j++)
prefixSum[i][j] += prefixSum[i][j-1];
}
// store indices of submatrix with maximum sum
int startCol = 0, endCol = 0, startRow = 0, endRow = 0;
int maxSum = INT_MIN;
// use Kadane's algorithm for finding maximum contiguous sum in 1D array
for(int firstCol=0;firstCol<m;firstCol++){
for(int secondCol=firstCol;secondCol<m;secondCol++){
int tmp[n]; // stores the sum between two columns for each row
for(int row=0;row<n;row++)
tmp[row] = prefixSum[row][secondCol] - (firstCol>0 ? prefixSum[row][firstCol-1] : 0);
int curSum = 0, curMaxSum = 0;
int curStartRow = 0, tmpStartRow = 0, curEndRow = -1;
for(int curRow=0;curRow<n;curRow++){
curSum += tmp[curRow];
if(curSum < 0) {
curSum = 0;
tmpStartRow = curRow+1;
} else if(curSum > curMaxSum) {
curMaxSum = curSum;
curStartRow = tmpStartRow;
curEndRow = curRow;
}
}
if(curEndRow == -1) {
curMaxSum = tmp[0];
curStartRow = 0;
curEndRow = 0;
for(int i=1;i<n;i++){
if(tmp[i] > curMaxSum){
curMaxSum = tmp[0];
curStartRow = i;
curEndRow = i;
}
}
}
if(curMaxSum > maxSum){
maxSum = curMaxSum;
startCol = firstCol;
endCol = secondCol;
startRow = curStartRow;
endRow = curEndRow;
}
}
}
cout<<"Sub-matrix with max Sum"<<endl;
for(int i=startRow;i<=endRow;i++){
for(int j=startCol;j<=endCol;j++){
cout<<matrix[i][j]<<" ";
}
cout<<endl;
}
return maxSum;
}
int main(){
int t;cin>>t;
while(t--){
int n,m;cin>>n>>m;
vector<vector<int>> matrix(n,vector<int>(m));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
cin>>matrix[i][j];
}
int ans = findMaximumSubMatrix(matrix, n, m);
cout<<ans<<endl;
}
}2 3 3 1 2 3 4 5 6 7 8 -100 2 4 102 1545 87 989 -8989 -45 120 -855
Sub-matrix with max Sum 1 2 4 5 7 8 27 Sub-matrix with max Sum 102 1545 87 989 2723
Java Code
import java.util.*;
import java.lang.*;
import java.io.*;
class Main {
static int findMaximumSubMatrix(int[][] matrix, int n, int m){
// stores the prefixSum of rows
int[][] prefixSum = new int[n][m];
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
prefixSum[i][j] = matrix[i][j];
}
// calculation prefix sum for each row
for(int i=0;i<n;i++){
for(int j=1;j<m;j++)
prefixSum[i][j] += prefixSum[i][j-1];
}
int startCol = 0, endCol = 0, startRow = 0, endRow = 0;
int maxSum = Integer.MIN_VALUE;;
for(int firstCol=0;firstCol<m;firstCol++){
for(int secondCol=firstCol;secondCol<m;secondCol++){
int tmp[] = new int[n]; // stores the sum between two columns for each row
for(int row=0;row<n;row++)
tmp[row] = prefixSum[row][secondCol] - (firstCol>0 ? prefixSum[row][firstCol-1] : 0);
int curSum = 0, curMaxSum = 0;
int curStartRow = 0, tmpStartRow = 0, curEndRow = -1;
for(int curRow=0;curRow<n;curRow++){
curSum += tmp[curRow];
if(curSum < 0) {
curSum = 0;
tmpStartRow = curRow+1;
} else if(curSum > curMaxSum) {
curMaxSum = curSum;
curStartRow = tmpStartRow;
curEndRow = curRow;
}
}
if(curEndRow == -1) {
curMaxSum = tmp[0];
curStartRow = 0;
curEndRow = 0;
for(int i=1;i<n;i++){
if(tmp[i] > curMaxSum){
curMaxSum = tmp[0];
curStartRow = i;
curEndRow = i;
}
}
}
if(curMaxSum > maxSum){
maxSum = curMaxSum;
startCol = firstCol;
endCol = secondCol;
startRow = curStartRow;
endRow = curEndRow;
}
}
}
System.out.println("Sub-matrix with max Sum");
for(int i=startRow;i<=endRow;i++){
for(int j=startCol;j<=endCol;j++){
System.out.print(matrix[i][j]+" ");
}
System.out.println();
}
return maxSum;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while(t-- > 0){
int n = sc.nextInt();
int m = sc.nextInt();
int matrix[][] = new int[n][m];
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
matrix[i][j] = sc.nextInt();
}
int ans = findMaximumSubMatrix(matrix, n, m);
System.out.println(ans);
}
}
}2 3 3 1 2 3 4 5 6 7 8 -100 2 4 102 1545 87 989 -8989 -45 120 -855
Sub-matrix with max Sum 1 2 4 5 7 8 27 Sub-matrix with max Sum 102 1545 87 989 2723
Complexity Analysis
Time Complexity: O(N^3)
The maximum sum rectangle in a 2D matrix problem has a polynomial-time complexity of O(N^3) because there are three nested loops. Two for fixing columns and one for Kadane’s Algorithm.
Space Complexity: O(N^2)
Since we made a 2D prefix Sum array. We have space complexity of O(N^2).