Maximum Subarray Sum Excluding Certain Elements

Table of Contents

Problem Statement

We are given an array, and we need to find maximum subarray sum excluding certain elements. That is, we need to find the max sum of subarray such that the subarray we are considering does not contain the elements which are told to be excluded.

Example of maximum subarray sum excluding certain elements

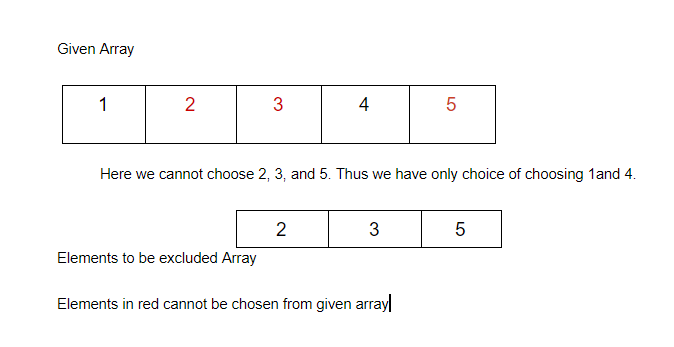
Array = {1,2,3,4,5}
Elements to be excluded = {2,3,5}

Explanation: Here, we cannot choose a subarray such that the subarray contains the excluded elements. Thus we can choose either 1 or 4. But since 4 is greater than 1, 4 is our answer. Ans problem is asking for a subarray instead of subsequence. Else we would have taken 1 in our answer as well.

Array = {1,-1,10,-6,2}
Elements to be excluded = {10}

Explanation: Here, we should not have chosen any negative element, and we cannot take 10 into subarray. So again, we have two choices, either choose 1 or 2. Since 2 > 1, answer is 2.

Approach to find maximum subarray sum excluding certain elements

Naive Approach

We can easily consider all the subarray, and then check whether subarray contains an element which was to be excluded. If it does not contain any such element, we simply find the sum and update our answer. But this approach is not efficient. An efficient approach would have been if we used Kadane’s algorithm to find the maximum subarray. But we run Kadane’s only in those parts which do not contain the elements to be excluded. Now, the problem is how do we find if we need to exclude an element or not. We can loop over the array of elements to be excluded. And if the array contains the current element, we do not choose it else we move ahead. But this approach can be further optimized, which is told in the Efficient approach section.

Efficient Approach

We already discussed that we would be using Kadane’s algorithm to find the sum of the subarray. Whenever the current element is one of the elements to be excluded. We just ignore that element and move ahead, while updating the currentSum to 0. Now, there is still a problem of finding out if the current element needs to be excluded or not? To check if the element needs to be excluded or not. We use a hash set or unordered_set. If the set contains the current element, we skip it else we proceed. So, just to be clear, this unordered_set contains the elements to be excluded.

Code to find maximum subarray sum excluding certain elements

C++ code

#include <bits/stdc++.h>
using namespace std;

int main(){
  int testCases;cin>>testCases;
  while(testCases--){
    int inputSize;cin>>inputSize;
    int input[inputSize];
    for(int i=0;i<inputSize;i++)
      cin>>input[i];
    int excludedElementsSize;cin>>excludedElementsSize;
    unordered_set<int> excludedElements;
    for(int i=0;i<excludedElementsSize;i++){
      int excludedElement;cin>>excludedElement;
      excludedElements.insert(excludedElement);
    }

    int currentSum = 0, maximumSum = 0;

    for(int i=0;i<inputSize;i++){
      if(excludedElements.count(input[i])){
        currentSum = 0;
      } else {
          currentSum = max(currentSum + input[i], input[i]);
          maximumSum = max(currentSum, maximumSum);
      }
    }
    cout<<maximumSum<<endl;
  }
}

Java Code

import java.util.*;

class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
    	int testCases = sc.nextInt();
    	while(testCases-- > 0){
    		int inputSize = sc.nextInt();
    		int input[] = new int[inputSize];
    		for(int i=0;i<inputSize;i++)
    		    input[i] = sc.nextInt();
    		int excludedElementsSize = sc.nextInt();
    		HashSet<Integer> excludedElements = new HashSet<Integer>();
    		for(int i=0;i<excludedElementsSize;i++){
    		    int excludedElement = sc.nextInt();
    	       	    excludedElements.add(excludedElement);
    		}
    
    		int currentSum = 0, maximumSum = 0;
    
    		for(int i=0;i<inputSize;i++){
    	            if(excludedElements.contains(input[i])){
    			currentSum = 0;
                    } else {
                        currentSum = Math.max(currentSum + input[i], input[i]);
                        maximumSum = Math.max(currentSum, maximumSum);
                    }
    		}
    
    		System.out.println(maximumSum);
        }
    }
}

Complexity Analysis

Time Complexity: O(N)

Since we have simply traversed over the array and just used an unordered_set or HashSet for storing the elements to be excluded. We have an algorithm with linear time complexity of O(N).

Space Complexity: O(N)

A HashSet or unrdered_set takes memory proportional to the number of key-value pairs, and other than that, we have used a single array. Thus we have space complexity of O(N).