Tiling Problem

Difficulty Level Easy
Frequently asked in 24*7 Innovation Labs Amazon DE Shaw Delhivery PayPal
Dynamic Programming Fibonacci MathViews 3343

Problem Statement

The “Tiling Problem” states that you have a grid of size 2 x N and a tile of size 2 x 1. So, find the number of ways to tile the given grid.

Example

3
2

Explanation: 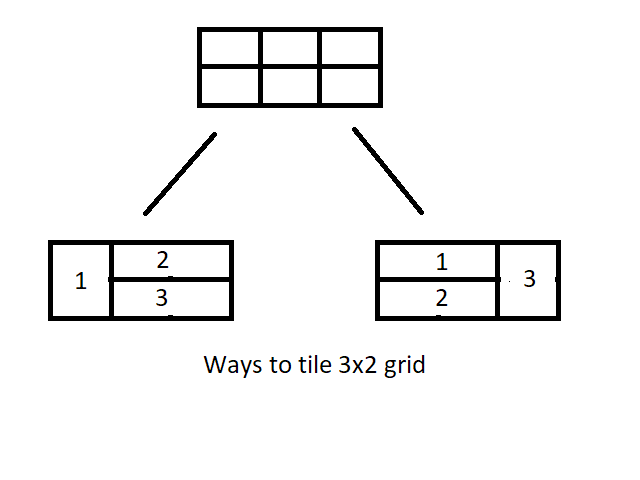Tiling Problem

Approach for Tiling Problem

We can solve this problem by using recursion. In the problem, we need to tile a grid of 2xN. So it will depend on the number of ways to tile grid of size 2x(N-1) and 2x(N-2). How can we say that?

The reason is simple, instead of thinking to tile the first column in grid then second and so on. We are trying to tile first the Nth column, then N-1 and so on. This way know that if we place a 2×1 tile on N th column. The problem is now converted to a sub-problem of tiling grid of size 2x(N-1). Similarly, if we place two 1×2 tiles in 2xN grid, the problem is converted to 2x(N-2) size. Now if we can somehow solve these problems, we can get the answer.

Let’s say Tile[N] denotes the number of ways to tile grid of size 2XN. Then Tile[N] = Tile[N-1] + Tile[N-2]. Similarly, Tile[N-1] = Tile[N-2] + Tile[N-3]. Thus the problem shows optimal substructure. It’s better to store the result for Tile[N-2] because it is being used twice. If we store the result, we will not compute it twice and will reduce the time complexity significantly. Thus we will use Dynamic Programming to solve the problem.

Tiling Problem

Code

C++ Code for Tiling Problem

#include<bits/stdc++.h> 
using namespace std; 

int main(){
  int n;cin>>n;
  // create an array to store number of ways to tile a grid of size 2xi
  int tile[n+1];
  // base case
  tile[0] = 0; tile[1] = 1;
  for(int i=2;i<=n;i++)
    tile[i]  = tile[i-1] + tile[i-2]; // use recursive formula
  cout<<tile[n];
}
3
2

Java code for Tiling Problem

import java.util.*;

class Main{
  
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    // create an array to store number of ways to tile a grid of size 2xi
    int tile[] = new int[n+1];
    // base case
    tile[0] = 0; tile[1] = 1;
    for(int i=2;i<=n;i++)
      tile[i]  = tile[i-1] + tile[i-2]; // use recursive formula
    System.out.println(tile[n]);
  }
}
3
2

Complexity Analysis

Time Complexity

O(N), because in order to solve the problem of tiling grid 2xN. You need to have calculated the answer for tiling grid of size less than N.

Space Complexity

O(N), because we are storing the result for all the subproblems and thus the space required is linear.

Note: We can solve the problem in O(1) space and O(N) time, by using two variables last and secondLast which will store the values of Tile[N-1] and Tile[N-2] respectively. Now current = last + secondLast and then update the values of the variables accordingly. The recursive formula is same as that of Nth Fibonacci number. So you can also solve this problem O(log N) time using formula to find Fibonacci numbers.

Translate »