Table of Contents
Problem statement
In the problem ” Minimum Score Triangulation of Polygon” we are given a value array where each element in the array represents the value of a N-sided polygon when labeled in a clockwise direction.
Our task is to triangulate the polygon into N-2 triangles. The score to triangulate a triangle is the product of the values at its three vertices. The total score to triangulate a polygon is the sum of all scores of all the triangulation.
We have to find the minimum score of triangulation of a polygon.
Example
values = [1,3,1,4,1,5]
13
Explanation: We will get a minimum score for triangulation when we triangulate the polygon in this way:
1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13
Approach for Minimum Score Triangulation of Polygon Leetcode Solution
Keeping in mind that we have to triangulate the polygon into N-2 triangles and the triangles Should not be overlapping. Every edge of the polygon can be a part of at most one triangle as overlapping is not allowed.
So every edge of the polygon can form a triangle with N-2 remaining vertices. Refer to the image below.
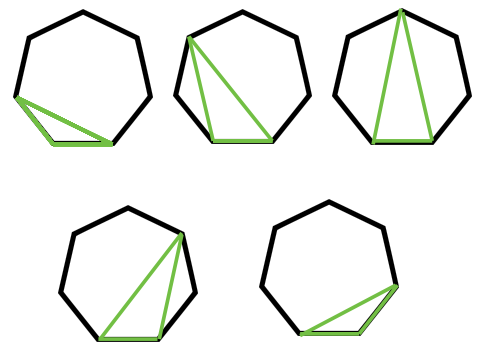
When we cut a triangle from the polygon we are left with a new smaller polygon. This led us to the point that we can break a problem into smaller subproblems.
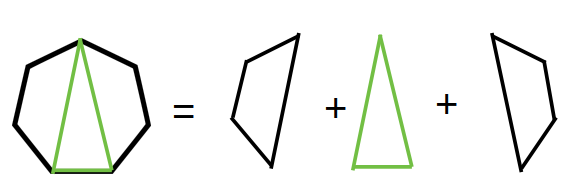
So if we want a minimum score for a polygon with vertex from 0-6 then the new subproblem is the minimum score for a polygon with vertex from 0-3 and 3-6.
hence the recursive relation becomes:
minScore( pos1, pos2) = minScore(pos1,i,A) + minScore(i,pos2,A) + A[pos1]*A[pos2]*A[i]
To overcome the recomputation of the same subproblem again and again we will use a memorization table. This will be a n*n array where the value at i,j will store the minimum score triangulation of polygon with vertices from i to j.
Implementation
C++ code for Minimum Score Triangulation of Polygon
#include <bits/stdc++.h>
using namespace std;
int memo[51][51];
int dp(int pos1,int pos2, vector<int>&A){
if(pos2-pos1<=1)return 0;
if(memo[pos1][pos2]!=-1)return memo[pos1][pos2];
int ans=INT_MAX;
for(int i=pos1+1;i<pos2;i++)
ans=min(ans, dp(pos1,i,A) + dp(i,pos2,A) + A[pos1]*A[pos2]*A[i] );
memo[pos1][pos2]=ans;
return ans;
}
int minScoreTriangulation(vector<int>& A) {
memset(memo,-1,sizeof(memo));
return dp(0,A.size()-1,A);
}
int main()
{
vector<int> arr = {1,3,1,4,1,5};
cout<<minScoreTriangulation(arr)<<endl;
return 0;
}13
Java code for Minimum Score Triangulation of Polygon
import java.util.Arrays;
public class Tutorialcup {
public static int minScoreTriangulation(int[] A) {
return dp(A, 0, A.length - 1, new Integer[A.length][A.length]);
}
public static int dp(int[] A, int pos1,int pos2, Integer[][] memo){
if(pos2-pos1<=1)return 0;
if(memo[pos1][pos2] != null)return memo[pos1][pos2];
int ans=Integer.MAX_VALUE;
for(int i=pos1+1;i<pos2;i++)
ans=Math.min(ans, dp(A,pos1,i,memo) + dp(A,i,pos2,memo) + A[pos1]*A[pos2]*A[i] );
memo[pos1][pos2]=ans;
return ans;
}
public static void main(String[] args) {
int [] arr = {1,3,1,4,1,5};
int ans= minScoreTriangulation(arr);
System.out.println(ans);
}
}13
Complexity Analysis of Minimum Score Triangulation of Polygon Leetcode Solution
Time complexity
The time complexity of the above code is O(n*n*n) because we are traversing the value array for 3 different i,j,k values that give a minimum score for triangulation of the polygon. Here n is the length of the value array.
Space complexity
The space complexity of the above code is O(n*n) because using n*n extra space for memorization.