Table of Contents
Problem Statement
In running sum of 1d array problem we have been given an array nums for which we have to return an array where for each index i in the result array arr[i] = sum( nums[0] … nums[i] ).
Example
nums = [1,2,3,4]
[1,3,6,10]
Explanation:
Running sum is : [1, 1+2, 1+2+3, 1+2+3+4] = [ 1, 3, 6, 10 ]
nums = [1,1,1,1,1]
[1,2,3,4,5]
Explanation:
Running sum is : [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1] = [ 1, 2, 3, 4, 5 ]
Approach
In this problem we have to create an array where value of element at index i will be equal to sum of the elements from 1st to the ith indexed element in given array.
For this we can simply create an array of size equal to given array size. Then for each element in a for loop we can add element from index 0 to index i in the original array using another for loop. Time complexity for this algorithm will be O(n^2).
We can reduce the time complexity for this problem by using only single loop.
let nums be the given array and res be an array in which we are storing the running sum, then we can calculate res[i] as following :
res[i]= res[i-1] + nums[i].
example : nums = [1,2,3,4] is shown in figure below,
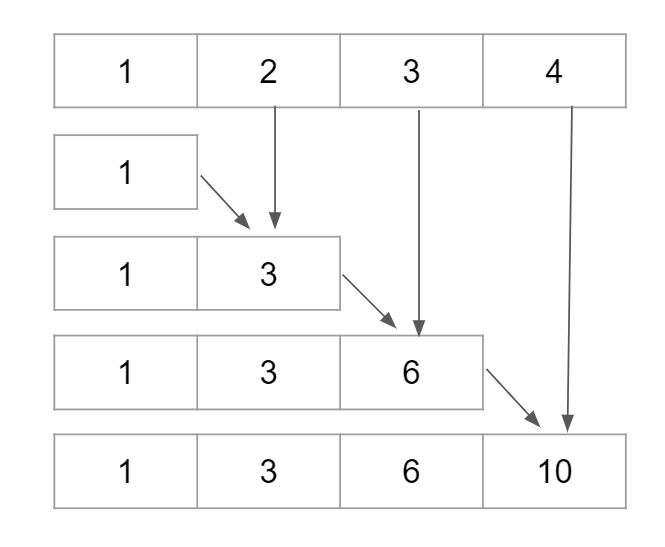
Hence we need not to run a for loop to calculate prefix sum again because we already have sum till index i stored in previous index of res array.
Implementation
C++ Program for Running Sum of 1d Array Leetcode Solution
#include <bits/stdc++.h>
using namespace std;
vector<int> runningSum(vector<int>& nums)
{
vector<int> res(nums.size());
if(nums.size()==0) return res;
res[0]=nums[0];
for(int i=1;i<nums.size();i++)
{
res[i]=res[i-1]+ nums[i];
}
return res;
}
int main()
{
vector<int> nums={1,2,3,4};
vector<int> res= runningSum(nums);
cout<<"[";
for(int i=0;i<res.size()-1;i++) cout<<res[i]<<",";
cout<<res.back()<<"]"<<endl;
return 0;
}[1,3,6,10]
Java Program for Running Sum of 1d Array Leetcode Solution
import java.lang.*;
class Rextester
{
public static int[] runningSum(int[] nums)
{
int[] res= new int[nums.length];
if(nums.length==0) return res;
res[0]=nums[0];
for(int i=1;i<nums.length;i++)
{
res[i]=res[i-1]+ nums[i];
}
return res;
}
public static void main(String args[])
{
int nums[]={1,2,3,4};
int res[]= runningSum(nums);
System.out.print("[");
for(int i=0;i<res.length-1;i++) System.out.print(res[i]+",");
System.out.println( res[res.length-1] + "]");
}
}[1,3,6,10]
Complexity Analysis for Running Sum of 1d Array Leetcode Solution
Time Complexity
O(n) : where n is the size of the given array. As we are running only a single for loop, hence time complexity will be linear.
Space Complexity
O(n) : Here we are creating a result array of size of n. Hence space complexity will also be linear.