Convert Sorted Array to Binary Search Tree Leetcode Solution

Difficulty Level Easy
Frequently asked in Adobe Airbnb Amazon Apple Bloomberg Cisco Google Microsoft Oracle Spotify VMware Yahoo
algorithms Binary Search Tree coding Depth First Search Interview interviewprep LeetCode LeetCodeSolutionsViews 3318

Consider we are given a sorted array of integers. The goal is to build a Binary Search Tree from this array such that the tree is height-balanced. Note that a tree is said to be height-balanced if the height difference of left and right subtrees of any node in the tree is at most 1.

It is easy to find that there can be multiple solutions. We need to find any valid solution. Note that in this problem, we do not need to print the tree but to create one. We just need to print its preorder traversal.

Example

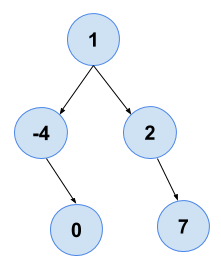
Array = {-4 , 0 , 1 , 2 , 7}
1 -4 0 2 7

Explanation: The BST is:

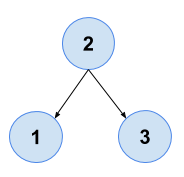
Convert Sorted Array to Binary Search Tree Leetcode Solution

 

Array = {1 , 2 , 3}
2 1 3

Explanation: The BST is:

Convert Sorted Array to Binary Search Tree Leetcode Solution

Approach(Recursion)

We need to keep track of two things:

  1. Any node should have smaller elements as left children and vice versa for right children
  2. The BST should be Height Balanced

In order to keep the tree balanced at any moment, we must choose a middle element of the array as the root. In this way, we will have a height difference of 1 between the left and right subtrees if the array is of even size and a height difference of 0 when the array is of an oddsize.

Now, when we select any middle node as root, we have to create the left subtree from the left subarray and right subtree from the right subarray. This is a sub-problem of our original problem and hence we can solve it recursively. After assigning left and right subtree to the middle node, we can return it and print the postorder traversal of the Binary Search Tree.

Algorithm

  1. Create another function converArrayToBST() which will convert any particular range of given array and return its corresponding BST root node.
  2. Let L = left limit of array and R = right limit of array in the above-mentioned range.
    1. If L > R
      • return NULL, as we receive a wrong range
    2. If L == R
      • return a new node having value same as Array[L] 
    3. Find the middle node of this range as mid = (L + (R – L) / 2)
      • Initialise head as a new BST Node with value same as Array[mid]
      • Assign left and right subtrees as the same function called on left and right sub-ranges respectively
      • Return head
  3. Print the preorder traversal of the Binary Search Tree

Implementation of Convert Sorted Array to Binary Search Tree Leetcode Solution

C++ Solution to Convert Sorted Array to Binary Search Tree

#include <bits/stdc++.h>
using namespace std;

struct BSTNode
{
    int value;
    BSTNode *left , *right;
    BSTNode(int x)
    {
        value = x;
        left = NULL;
        right = NULL;
    }
};

BSTNode* convertArrayToBST(vector <int> &a , int l , int r)
{
    if(l > r)
        return NULL;
    if(l == r)
        return new BSTNode(a[l]);
    int mid = (l + (r - l) / 2);
    BSTNode* head = new BSTNode(a[mid]);
    head->left = convertArrayToBST(a , l , mid - 1);
    head->right = convertArrayToBST(a , mid + 1 , r);
    return head;
}

BSTNode* sortedArrayToBST(vector<int>& a)
{
    int n = a.size();
    return convertArrayToBST(a , 0 , n - 1);
}

void preorder(BSTNode* head)
{
    if(!head)
        return;
    cout << head->value << " ";
    preorder(head->left);
    preorder(head->right);
}


int main()
{
    vector <int> a = {-4 , 0 , 1 , 2 , 7};
    BSTNode* head = sortedArrayToBST(a);
    preorder(head);
    return 0;
}

Java Solution to Convert Sorted Array to Binary Search Tree

class BSTNode
{
    int value;
    BSTNode left , right;
    BSTNode(int x)
    {
        value = x;
        left = null;
        right = null;
    }
}

class convert_array_to_BST
{
    public static void main(String args[])
    {
        int[] a = {-4 , 0 , 1 , 2 , 7};
        BSTNode head = sortedArrayToBST(a);
        preorder(head);
    }

    static BSTNode convertArrayToBST(int[] a , int l , int r)
    {
        if(l > r)
            return null;
        if(l == r)
            return new BSTNode(a[l]);
        int mid = (l + (r - l) / 2);
        BSTNode head = new BSTNode(a[mid]);
        head.left = convertArrayToBST(a , l , mid - 1);
        head.right = convertArrayToBST(a , mid + 1 , r);
        return head;
    }

    static BSTNode sortedArrayToBST(int[] a)
    {
        return convertArrayToBST(a , 0 , a.length - 1);
    }

    static void preorder(BSTNode head)
    {
        if(head == null)
            return;
        System.out.print(head.value + " ");
        preorder(head.left);
        preorder(head.right);
    }
}

1 -4 0 2 7

Complexity Analysis of Convert Sorted Array to Binary Search Tree Leetcode Solution

Time Complexity

O(N), N = Number of elements in the tree. We visit every element to construct the BST and to print the preorder traversal.

Space Complexity

O(H), where H = Height of the tree = logN. In both the recursive functions, we make sure that the tree is height-balanced, So, we use a maximum of O(H) space for recursive stack frames.

Translate »