Permutations Leetcode Solution

The problem Permutations Leetcode Solution provides a simple sequence of integers and asks us to return a complete vector or array of all the permutations of the given sequence. So, before going into solving the problem. We should be familiar with permutations. So, a permutation is nothing but an arrangement of given integers. So, when we say that we need all the permutations of a sequence. We mean that we are required to print or return all possible arrangements of the given sequence. Let’s take a look at a few examples for better understanding.

Given sequence: [1,2,3]

Permutations: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Explanation: All the ways that you can write 1, 2, 3 in a sequence have been given as output. There are a total of 6 ways to write 1, 2, 3 in a permutation.

[0,1]

[[0,1],[1,0]]

Explanation: There are only 2 ways possible to write 0, 1.

Backtracking Approach for Permutations Leetcode Solution

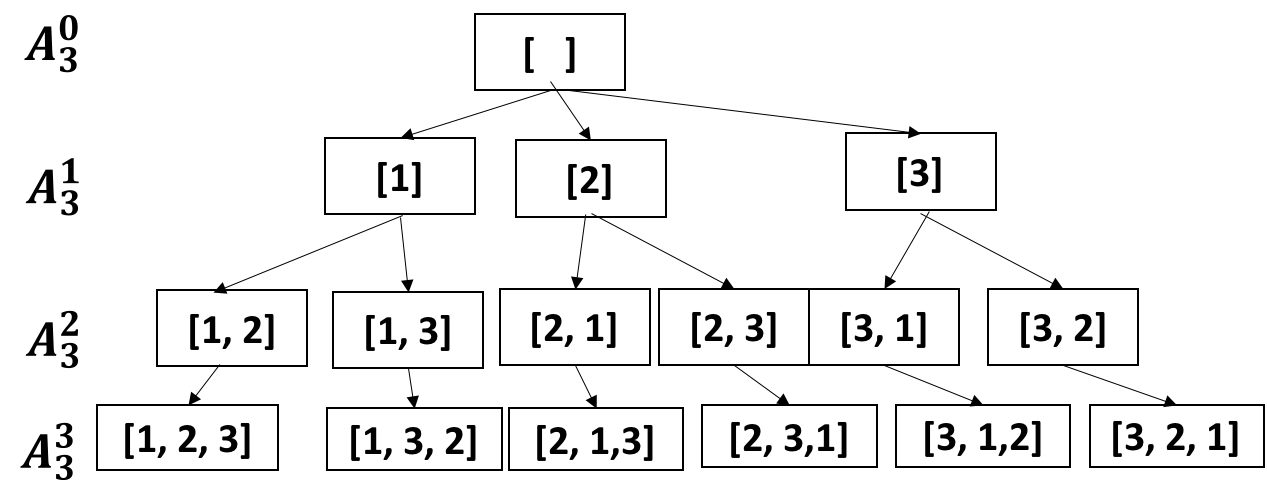
The problem Permutations Leetcode Solution asked us to generate all the permutations of the given sequence. Generally, we are required to generate a permutation or some sequence recursion is the key to go. But here the recursion or backtracking is a bit tricky. One way could have been picking an element from unpicked elements and placing it at the end of the answer. This way generate a permutation and somehow make sure to remember that this permutation has been generated and should not be repeated. But instead of doing this, we try to find a simple way to perform the task. What if we pick an element and swap it with the current element. Then make a recursive call to generate all the permutations for the sequence one index after the current index.

Once we are done with generating the permutations one index ahead. We remove the picked element, and then pick another element and repeat the procedure. This way we make sure that we have placed each unused element at least once in the current position. And since we made a recursive call to a smaller subproblem. The smaller subproblem being generating the permutation for the sequence starting just after the current index. Adding those permutations to the current permutation completes a set of permutation with an element set at the current index. This way we keep traversing the array from left to right and dividing the problem into smaller subproblems. Once we reach the need we have generated d a possible permutation and we add it to the answer.

Backtracking code

C++ code for Permutations Leetcode Solution

#include <bits/stdc++.h>
using namespace std;

void permutationUtil(vector<int> &nums, int i, int &numsSize, vector<vector<int>> &answer){
    if(i == numsSize){
        answer.push_back(nums);
    }
    for(int j = i; j < numsSize; j++){
        swap(nums[i], nums[j]);
        permutationUtil(nums, i+1, numsSize, answer);
        swap(nums[i], nums[j]);
    }
}

vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int>> answer;
    int numsSize = nums.size();
    permutationUtil(nums, 0, numsSize, answer);
    return answer;
}

int main(){
    vector<int> nums({1, 2, 3});
    vector<vector<int>> answer = permute(nums);
    for(auto i: answer){
        for(auto j: i)
            cout<<j<<" ";
        cout<<"\t";
    }
}

1 2 3   1 3 2   2 1 3   2 3 1   3 2 1   3 1 2

Java Code for Permutations Leetcode Solution

import java.util.*;
import java.lang.*;
import java.io.*;
 
class Main {
    public static void permutationUtil(List<Integer> nums, int i, int numsSize, List<List<Integer>> answer){
        if(i == numsSize){
            answer.add(new ArrayList<Integer>(nums));
        }
        for(int j = i; j < numsSize; j++){
            Collections.swap(nums, i, j);
            permutationUtil(nums, i+1, numsSize, answer);
            Collections.swap(nums, i, j);
        }
    }
 
    public static List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> answer = new LinkedList();
        int numsSize = nums.length;
        List<Integer> list = new ArrayList<Integer>();
        for(int i=0;i<numsSize;i++)
            list.add(nums[i]);
        permutationUtil(list, 0, numsSize, answer);
        return answer;
    }
 
    public static void main(String[] args){
    	int nums[] = {1, 2, 3};
    	List<List<Integer>> answer = permute(nums);
    	System.out.println(answer.toString());
    }
}

[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1], [3, 1, 2]]

Complexity Analysis

Time Complexity

O(Sigma(P(N,K)), where P is the k permutation of n or partial permutation. More formally, P(N, k) = (N!)/((N-k)!).

Space Complexity

O(N!), since we have to store all the possible solutions which are N! in size where N is the size of the array.