Table of Contents
Problem Statement
In this problem, we need to find the difference between the product of digits and the sum of digits of a given positive integer.
Example
1234
14
Explanation: Product = 4 * 3 * 2 * 1 = 24 and Sum = 4 + 3 + 2 + 1 = 10. So, the difference is 14
2045
-11
Explanation: Product = 2 * 0 * 4 * 5 = 0 and Sum = 2 + 0 + 4 + 5 = 11. So, the difference is -11.
Approach
It becomes easy to return the desired output if we could extract out the digits from the integer one by one. This can be easily done by using the ‘%’ operator, as ” % 10 ” fetchs us the last digit of an integer, we can then divide the integer by 10 to pop the last digit out of it(as we did it in this problem). In this way, we can process each digit and find the product and the sum. Then, we can return the difference between them to get the required result.
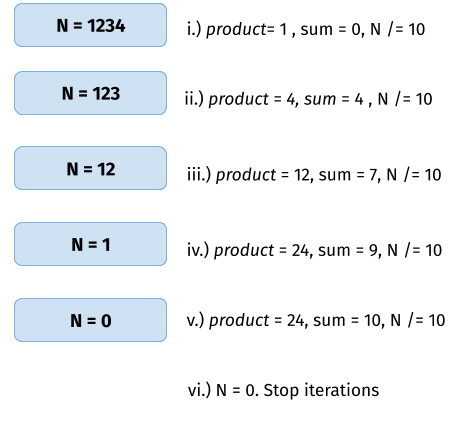
Algorithm
- Initialize two variables, product = 1 and sum = 0 to store the product and sum of digits of integer N respectively
- Follow these steps until N > 0:
- Multiply the last digit of N to product, product *= N % 10
- Add the last digit of N to sum, sum += N % 10
- Divide N by 10 to drop the last digit, N /= 10
- Return product – sum
Implementation of Subtract the Product and Sum of Digits of an Integer Leetcode Solution
C++ Program
#include <bits/stdc++.h>
using namespace std;
int subtractProductAndSum(int n)
{
int product = 1 , sum = 0;
while(n > 0)
{
//n % 10 extracts the last digit out of N
product *= (n % 10);
sum += (n % 10);
n /= 10;
}
return product - sum;
}
int main()
{
int n = 1234;
cout << subtractProductAndSum(n) << '\n';
return 0;
}
Java Program
class subtract_product_and_sum
{
public static void main(String args[])
{
int n = 1234;
System.out.println(subtractProductAndSum(n));
}
static int subtractProductAndSum(int n)
{
int product = 1 , sum = 0;
while(n > 0)
{
//n % 10 extracts the last digit out of N
product *= (n % 10);
sum += (n % 10);
n /= 10;
}
return product - sum;
}
}14
Complexity Analysis of Subtract the Product and Sum of Digits of an Integer Leetcode Solution
Time Complexity
O(log2N) as we loop for every digit in an integer N.
Space Complexity
O(1) as we use constant memory space.