Table of Contents
Problem Statement
Maximum Number of Ways to Partition an Array LeetCode Solution – You are given a 0-indexed integer array nums of length n. The number of ways to partition nums is the number of pivot indices that satisfy both conditions:
1 <= pivot < nnums[0] + nums[1] + ... + nums[pivot - 1] == nums[pivot] + nums[pivot + 1] + ... + nums[n - 1]
You are also given an integer k. You can choose to change the value of one element of nums to k, or to leave the array unchanged.
Return the maximum possible number of ways to partition nums to satisfy both conditions after changing at most one element.
Input: nums = [2,-1,2], k = 3 Output: 1 Explanation: One optimal approach is to change nums[0] to k. The array becomes [3,-1,2]. There is one way to partition the array: - For pivot = 2, we have the partition [3,-1 | 2]: 3 + -1 == 2.
Explanation
First, if we do not change any number, how many ways we can split this array A into two parts with an equal sum? We can get the prefix sum array of A, and count how many occurrences of sum(A) / 2 in the prefix sum array. (If sum(A) % 2 = 1 meaning there is no way to split it)
Take a look at the array A in the picture below as an example.
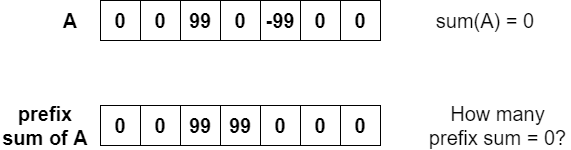
Once we get the prefix sum of A, and the sum of A which is 0, let’s count how many 0s in prefix sum. Notice that we NEVER count the last prefix sum since it stands for A itself.
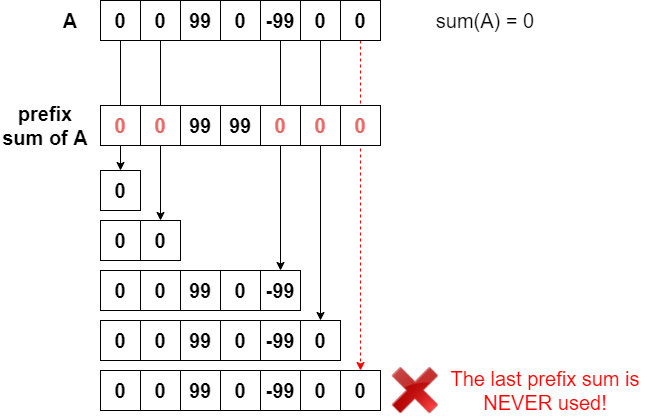
We find 4 0 in the prefix sum array. That means without changing a number, there are 4 ways to split it.
What if we change one number, let’s say A[i], can we still get the number of splitting ways by counting the occurrence of half the sum, or by some similar methods? Yes.
Take the array A below is an example. Suppose we changed A[4] from 3 to 4, how will the prefix sum array change according to the change of one number?
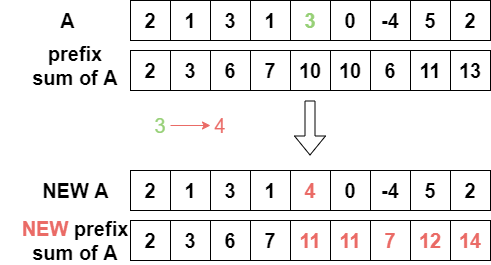
We can tell that ONLY the prefix sum of and after A[4] are changed. Since A[4] is added by one, all the changed prefix sums are added by one as well.
We use two hashmaps(let’s call them pred and sufd) to store the occurrence of all prefix sum of the Original A, we don’t change any key of either hashmap because it will bring O(N^2) time complexity and there is no need to change it.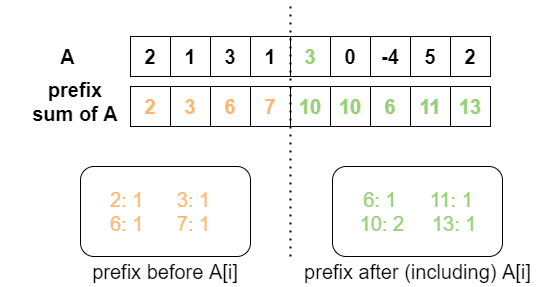
Now, once we have changed A[4] from 3 to 4, what is the next step to finding all splitting ways? Similarly, we look for occurrences of half sum in the hashmap.
- When we look into pred, we search of the occurrence of
newSum / 2. - When we look into sufd, we don’t search for
newSum / 2, but(newSum - k + A[i]) / 2.
Why?
Remember that we do not update the keys in either of the hashmaps, thus they only contain the information of the original A. When we want to get the result of newSum / 2, we have to modify it by A[i] - k which is the reverse value by which the original A has changed.
Don’t forget to update the occurrence of this presum pre[i] in both hashmaps. That is, “move” one pre[i] from sufd to pred and move on for the next index.
Code
C++ Code For Maximum Number of Ways to Partition an Array
class Solution {
public:
int waysToPartition(vector<int>& A, int k) {
int n = A.size();
long long s = 0, ans = 0;
vector<int> pre;
unordered_map<long long, long long> pred, sufd;
for (int a : A) {
s += a;
pre.push_back(s);
sufd[s] += 1;
}
sufd[s] -= 1;
if (s % 2 == 0) {
ans += sufd[s / 2];
}
for (int i = 0; i < n; ++i) {
long long cur = 0;
if (A[i] != k) {
int news = s + k - A[i];
if (news % 2 == 0) {
if (i > 0)
cur += pred[news / 2];
if (i < n - 1)
cur += sufd[news / 2 + A[i] - k];
}
}
ans = max(ans, cur);
sufd[pre[i]] -= 1;
pred[pre[i]] += 1;
}
return ans;
}
};
Java Code For Maximum Number of Ways to Partition an Array
public int waysToPartition(int[] nums, int k) {
int n = nums.length;
int[] pref = new int[n];
pref[0] = nums[0];
Map<Integer, Integer> count = new HashMap<>(); //contribution of prefixes without changing
count.put(pref[0], 1);
for (int i = 1; i < n - 1; i++){
pref[i] += pref[i - 1] + nums[i];
count.put(pref[i], count.getOrDefault(pref[i], 0) + 1);
}
pref[n - 1] += pref[n - 2] + nums[n - 1]; //last step doesn't add into 'count' map, because we're trying to find at least two parts.
int sum = pref[n - 1];
int max = 0;
if (sum % 2 == 0)
max = count.getOrDefault(sum / 2, 0); //max without changing
Map<Integer, Integer> countPrev = new HashMap<>(); //contribution of prefixes before current step
for (int i = 0; i < n; i++){
int diff = k - nums[i];
int changedSum = sum + diff;
if (changedSum % 2 == 0)
max = Math.max(max, count.getOrDefault(changedSum / 2 - diff, 0) + countPrev.getOrDefault(changedSum / 2, 0));
count.put(pref[i], count.getOrDefault(pref[i], 0) - 1);
countPrev.put(pref[i], countPrev.getOrDefault(pref[i], 0) + 1);
}
return max;
}
Python Code For Maximum Number of Ways to Partition an Array
class Solution:
def waysToPartition(self, A: List[int], k: int) -> int:
n = len(A)
pre, s = list(itertools.accumulate(A)), sum(A)
ans = 0
# pred contains all the presum BEFORE i-th number.
# sufd contains all the presum AFTER and WITH i-th number.
pred = collections.defaultdict(int)
sufd = collections.Counter(pre)
# The last prefix sum is NEVER used.
sufd[sum(A)] -= 1
# The number of ways if we do not change any number.
if s % 2 == 0:
ans = sufd[s // 2]
# The number of ways if we split i-th number to k.
for i in range(n):
cur = 0
# We only count number of ways when A[i] != k (otherwise change makes no difference)
# and when the SUM after the change is dividable by 2.
if A[i] != k:
news = s + k - A[i]
if news % 2 == 0:
# If i == 0, only count suffix part.
if i > 0:
cur += pred[news // 2]
# If i == n - 1, only count prefix part.
if i < n - 1:
cur += sufd[news // 2 + A[i] - k]
ans = max(ans, cur)
# Don't forget to change the values in the two counters.
sufd[pre[i]] -= 1
pred[pre[i]] += 1
return ans
Complexity Analysis for Maximum Number of Ways to Partition an Array LeetCode Solution
Time Complexity
O(N) we would take each i from 0 to n-1 as a pivot and check.
Space Complexity
O(N) if all prefix sums will be different then there would be at max n keys in the hashmap.