Table of Contents
Problem Statement
“Maximum Side Length of a Square with Sum Less than or Equal to Threshold,” says that a m x n matrix mat and an integer threshold are given, return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.
Example 1:
 Input:
Input:
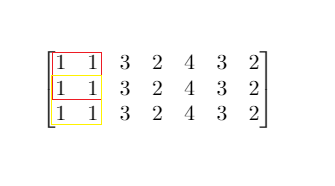
mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output:
2
Explanation:
The maximum side length of square with sum less than 4 is 2 as shown.
Example 2:
Input:
mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output:
0
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 3000 <= mat[i][j] <= 1040 <= threshold <= 105
Approach
Idea
1. This problem can be solved using the binary-search and prefix sum method.
2. pre[i][j] is the sum of all elements from rectangle (0,0,i,j) as left,top,right,bottom.
3. To calculate the pref[i][j], we will use this relation pre[i][j]=pre[i-1][j]+pre[i][j-1]+mat[i-1][j-1]-pre[i-1][j-1].
4. Since the value in the matrix is positive, so we can use binary search to find the appropriate square length k.
5. Now we will make a check function and simulate our answer as it’s satisfied or not.
6. See the below code for better visualization.
Code
Maximum Side Length of a Square with Sum Less than or Equal to Threshold LeetCode C++ Solution
class Solution {
public:
#define ll long long
ll check(ll len,vector<vector<ll>>&a,ll yo,ll n,ll m)
{
ll i,j;
for(i=len;i<=n;i++)
{
for(j=len;j<=m;j++)
{
if (a[i][j] - a[i-len][j] - a[i][j-len] + a[i-len][j-len] <= yo) return 1;
}
}
return 0;
}
int maxSideLength(vector<vector<int>>& mat, int threshold) {
ll n=mat.size(),m=mat[0].size();
vector<vector<ll>>pre(n+1,vector<ll>(m+1,0));
ll i,j;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
pre[i][j]=pre[i-1][j]+pre[i][j-1]+mat[i-1][j-1]-pre[i-1][j-1];
}
}
ll l=1,r=min(n,m),mid,ans=0;
while(l<=r)
{
mid=l+(r-l)/2;
if(check(mid,pre,threshold,n,m))
{
l=mid+1;
ans=mid;
}
else
{
r=mid-1;
}
}
return ans;
}
};Maximum Side Length of a Square with Sum Less than or Equal to Threshold LeetCode Java Solution
class Solution {
int[][] pre = new int[302][302];
int check(int len,int yo,int n,int m)
{
int i,j;
for(i=len;i<=n;i++)
{
for(j=len;j<=m;j++)
{
if (pre[i][j] - pre[i-len][j] - pre[i][j-len] + pre[i-len][j-len] <= yo) return 1;
}
}
return 0;
}
public int maxSideLength(int[][] mat, int threshold) {
int n=mat.length,m=mat[0].length;
int i,j;
for(i=0;i<=n;i++)
for(j=0;j<=m;j++)
pre[i][j]=0;
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
pre[i][j]=pre[i-1][j]+pre[i][j-1]+mat[i-1][j-1]-pre[i-1][j-1];
}
}
int l=1,r=Math.min(n,m),mid,ans=0;
while(l<=r)
{
mid=l+(r-l)/2;
if(check(mid,threshold,n,m)==1)
{
l=mid+1;
ans=mid;
}
else
{
r=mid-1;
}
}
return ans;
}
}
Complexity analysis:
Time Complexity
Time complexity is O(m*n*log(min(m,n))), where m,n is the dimension of the array. Log factor comes due to binary search and check function is O(m*n).
Space Complexity
Space complexity is O(m*n).where m,n is the dimension of the array. We are taking extra space to precompute the array.