Table of Contents
Problem Statement:
Step-By-Step Directions From a Binary Tree Node to Another LeetCode Solution – You are given the root of a binary tree with n nodes. Each node is uniquely assigned a value from 1 to n. You are also given an integer startValue representing the value of the start node s, and a different integer destValue representing the value of the destination node t.
Find the shortest path starting from the node s and ending at the node t. Generate step-by-step directions of such path as a string consisting of only the uppercase letters 'L', 'R', and 'U'. Each letter indicates a specific direction:
'L'means to go from a node to its left child node.'R'means to go from a node to its right child node.'U'means to go from a node to its parent node.
Return the step-by-step directions of the shortest path from the node s to node t.
Examples:
Input:
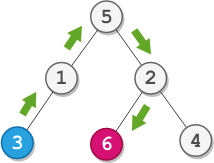
root = [5,1,2,3,null,6,4], startValue = 3, destValue = 6
Output:
"UURL"
Explanation:
The shortest path is: 3 → 1 → 5 → 2 → 6.
Approach:
Idea:
The idea is to first find the path of source and destination from the root. This can be done by a simple DFS traversal. Once we have the paths to the source and destination then we will be removing that part of the path which is common to both the source and destination. That is we only need the path of the source and destination when approached from their lowest common ancestor.
The length of the path to the source node will denote the number of up movements i.e., “U” we need to do in order to reach the lowest common ancestor. Once we get the count of this we can simply append the destination node path to this. This will be our final answer. Check out the C++ code for a better understanding,
Another method for solving this problem is to first generate a graph out of the tree and then simply do a BFS from the source until we reach the destination node. To create the graph we will be doing another BFS and will be storing the movement we did in order to reach a particular node, i.e., left or right and this thing will change to up when seen from the child node perspective. Check out the Python code for a better understanding.
Code:
Step-By-Step Directions From a Binary Tree Node to Another C++ Solution:
class Solution {
public:
bool dfs(TreeNode* root, int target, string &path){
if(root->val == target){
return true;
}
if(root->left){
path.push_back('L');
if(dfs(root->left,target,path))
return true;
path.pop_back();
}
if(root->right){
path.push_back('R');
if(dfs(root->right,target,path))
return true;
path.pop_back();
}
return false;
}
void removePrefix(string &s1,string &s2){
int n1 = s1.length();
int n2 = s2.length();
int i=0;
while(i<min(n1,n2) and s1[i]==s2[i])
i++;
s1 = s1.substr(i);
s2 = s2.substr(i);
}
string getDirections(TreeNode* root, int startValue, int destValue) {
string pathOne = "";
string pathTwo = "";
dfs(root,startValue,pathOne);
dfs(root,destValue,pathTwo);
removePrefix(pathOne,pathTwo);
int n = pathOne.length();
string s = "";
for(int i=0;i<n;i++){
s.push_back('U');
}
s += pathTwo;
return s;
}
};Step-By-Step Directions From a Binary Tree Node to Another Python Solution:
class Solution:
def getDirections(self, root: Optional[TreeNode], s: int, d: int) -> str:
graph = collections.defaultdict(list)
q = collections.deque([root])
# create graph
while q:
node = q.popleft()
if node.left:
graph[node.val].append((node.left.val,'L'))
graph[node.left.val].append((node.val,'U'))
q.append(node.left)
if node.right:
graph[node.val].append((node.right.val,'R'))
graph[node.right.val].append((node.val,'U'))
q.append(node.right);
q = collections.deque([(s,"")])
vis = set()
# BFS from source to destination
while q:
for i in range(len(q)):
top = q.popleft()
for it in graph[top[0]]:
val = it[0]
dirs = it[1]
if val not in vis:
path = top[1]
path += dirs;
if val==d:
return path
q.append((val,path))
vis.add(top[0])
return ""
Complexity Analysis of Step-By-Step Directions From a Binary Tree Node to Another LeetCode Solution:
- Time Complexity: The time complexity of the above C++ code is O(n).
- Space Complexity: The space complexity of the above C++ code is O(n).