Table of Contents
Problem Statement
Valid Triangle Number LeetCode Solution – Given an integer array nums, return the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle.
Input: nums = [2,2,3,4] Output: 3 Explanation: Valid combinations are: 2,3,4 (using the first 2) 2,3,4 (using the second 2) 2,2,3
Explanation
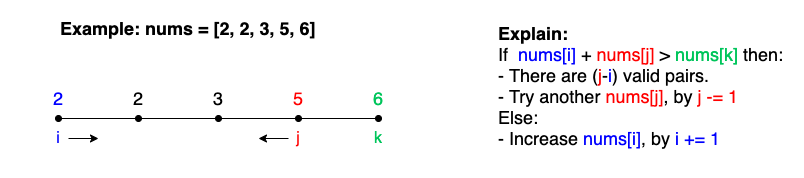
Once we sort the given array, we need to find the right limit of the index k for a pair of indices (i, j) chosen to find the count of elements satisfying nums[i] + nums[j] > nums[k] for the triplet (nums[i], nums[j], nums[k]) to form a valid triangle.
We can find this right limit by simply traversing the index ‘s values starting from the index k=j+1 for a pair (i, j) chosen and stopping at the first value of k not satisfying the above inequality. Again, the count of elements nums[k] satisfying nums[i] + nums[j] > nums[k] for the pair of indices (i, j) chosen is given by k – j – 1 as discussed in the last approach.
Further, as discussed in the last approach, when we choose a higher value of index j for a particular i chosen, we need not start from the index j + 1. Instead, we can start off directly from the value of k where we left for the last index j. This helps to save redundant computations.
Code for Valid Triangle Number LeetCode Solution
Java Code:
public class Solution {
public int triangleNumber(int[] nums) {
int count = 0;
Arrays.sort(nums);
for (int i = 0; i < nums.length - 2; i++) {
int k = i + 2;
for (int j = i + 1; j < nums.length - 1 && nums[i] != 0; j++) {
while (k < nums.length && nums[i] + nums[j] > nums[k])
k++;
count += k - j - 1;
}
}
return count;
}
}C++ Code:
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int n = nums.size(), ans = 0;
for (int k = 2; k < n; ++k) {
int i = 0, j = k - 1;
while (i < j) {
if (nums[i] + nums[j] > nums[k]) {
ans += j - i;
j -= 1;
} else {
i += 1;
}
}
}
return ans;
}
};Complexity Analysis for Valid Triangle Number LeetCode Solution
Time Complexity
O(n^2)
Space Complexity
O(1)