Given an integer array and an integer k. Find total number of contiguous subarrays of given array whose sum of elements is equal to k.
Table of Contents
Example
Input 1: arr[] = {5,0,5,10,3,2,-15,4}
k = 5
Output: 7
Input 2: arr[] = {1,1,1,2,4,-2}
k = 2
Output: 4
Explanation : consider example-1 given above,the image below highlights all the subarrays with given sum k( = 5).
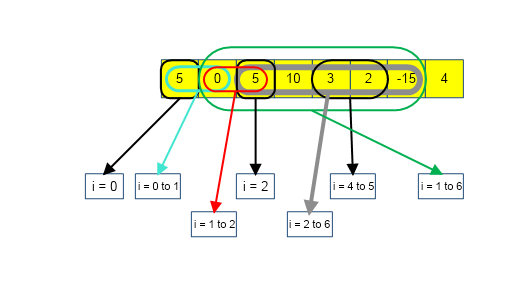
Types of solution
- Brute Force/Naive
- Using cumulative sum
- without using extra space
- Using Hash Map data structure
Brute Force/Naive
Approach
The idea is to generate all the subarrays of the given array and check whether sum of elements of the subarray is equal to given k. If sum of the subarray elements is equal to given k then increment the value of count used to store the required result.
Algorithm
- Run outer loop from range[0 to n-1]. Loop variable is start.
- Run inner loop from range[start+1,n]. Loop variable is end.
- Run a loop nested into the above loop from range[start,end-1] and calculate the sum in this range.
- If sum equals to given k, then increase the value of count.
The above algorithm is depicted below :
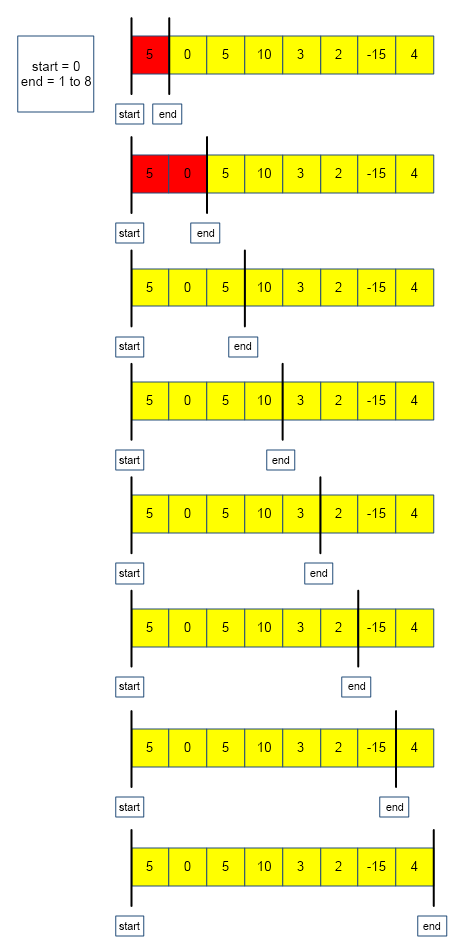
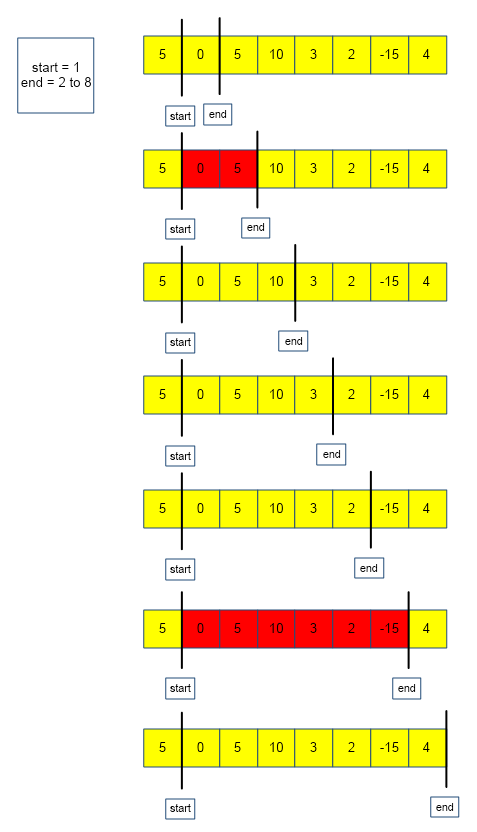
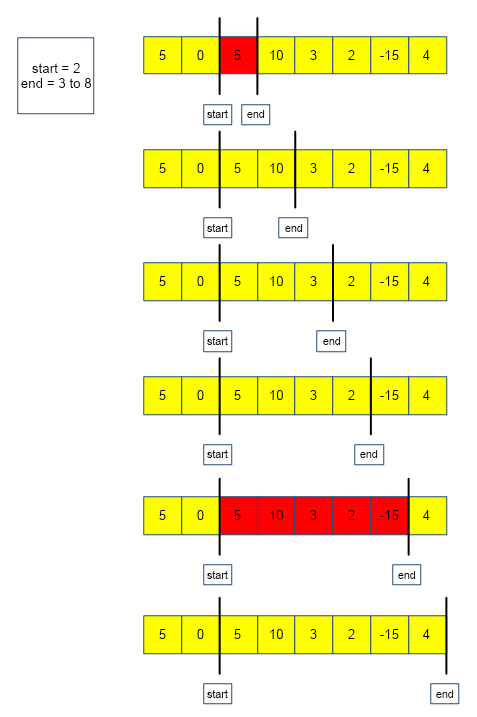
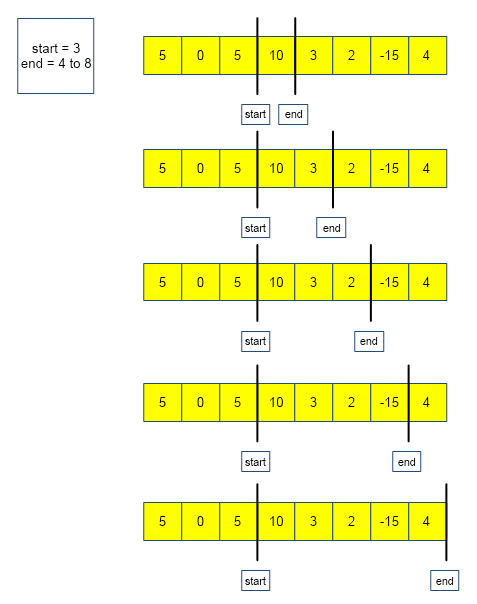
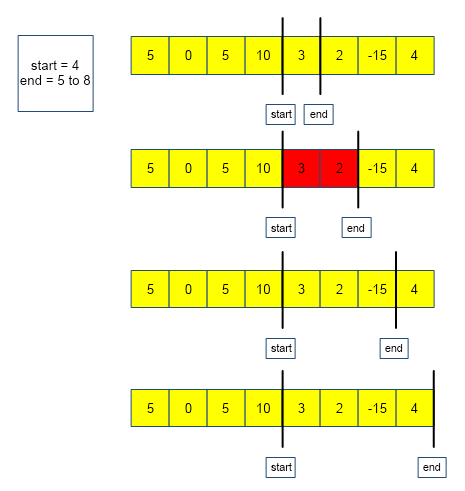
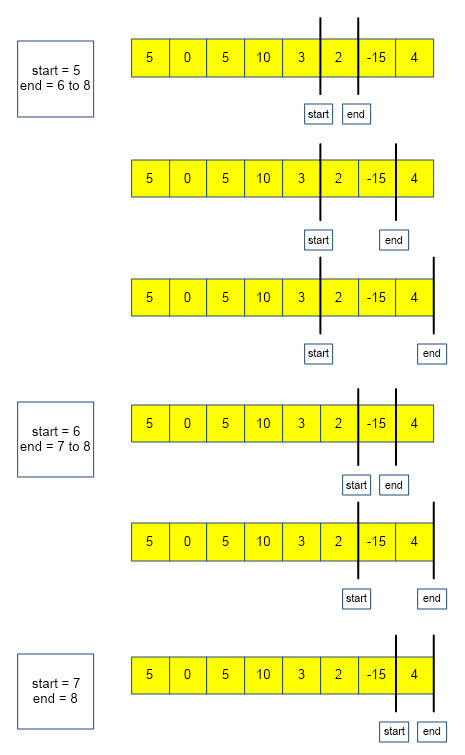
From the above images, we observe that there are in total 7 subarrays (highlighted in red) that have the given sum(k = 5).
Implementation
C++ Program For Subarray sum equals k
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// function to find number of subarrays with sum = k
int subArraySum(vector <int> arr,int k)
{
int n = arr.size();
int count = 0;
// generate all the subarrays
// a given subarray within range [start,end]
// is chosen
for(int start=0;start<n;start++)
{
for(int end=start+1;end<=n;end++)
{
int sum = 0;
// find sum of the elements in range[start,end]
for(int i=start;i<end;i++)
sum += arr[i];
// if the given sum equals to k
// then increment the required count value
if(sum == k)
count++;
}
}
return count;
}
// main program to implement above functions
int main()
{
vector <int> arr = {5,0,5,10,3,2,-15,4};
int k = 5;
cout<<"Number of subarrays with sum equal to "<<k<<" = "<<subArraySum(arr,k)<<endl;
return 0;
}Output
Number of subarrays with sum equal to 5 = 7
Java Program For Subarray sum equals k
import java.io.*;
import java.util.*;
class tutorialCup
{
// function to find number of subarrays with sum = k
static int subArraySum(ArrayList <Integer> arr,int k)
{
int n = arr.size();
int count = 0;
// generate all the subarrays
// a given subarray within range [start,end]
// is chosen
for(int start=0;start<n;start++)
{
for(int end=start+1;end<=n;end++)
{
int sum = 0;
// find sum of the elements in range[start,end]
for(int i=start;i<end;i++)
sum += arr.get(i);
// if the given sum equals to k
// then increment the required count value
if(sum == k)
count++;
}
}
return count;
}
// main program to implement above functions
public static void main (String[] args)
{
ArrayList <Integer> arr = new ArrayList<Integer>(Arrays.asList(5,0,5,10,3,2,-15,4));
int k = 5;
System.out.println("Number of subarrays with sum equal to "+k+" = "+subArraySum(arr,k));
}
}
Output
Number of subarrays with sum equal to 5 = 7
Complexity Analysis
- Time Complexity : T(n) = O(n3)
- Space Complexity : A(n) = O(1)
Using cumulative sum
Approach
Instead of generating all the subarrays and calculating their sum. We use a cumulative sum array sum[] wherein sum[i] stores sum of all array elements until index (i-1). Then, in order to calculate the sum of elements lying between two indices(i and j), we can subtract the cumulative sum(sum[i] – sum[j-1]) corresponding to the two indices to obtain the sum directly.
Algorithm For Subarray sum equals k
- create a cumulative sum array sum[] of length n+1 (n = size of of input array arr[]).
- assign sum[0] = 0, sum of zero elements.
- Iterate over arr[] and assign sum[i] = sum of elements in range[0,i-1].
- Run an outer loop in range[0,n-1]. Loop variable is start.
- Run an inner loop in range[start+1,n]. Loop variable is end.
- Sum of elements in range[start,end] = sum[end] – sum[start].
- If this sum is equal to k, then increment the count variable.
The above algorithm is depicted below :
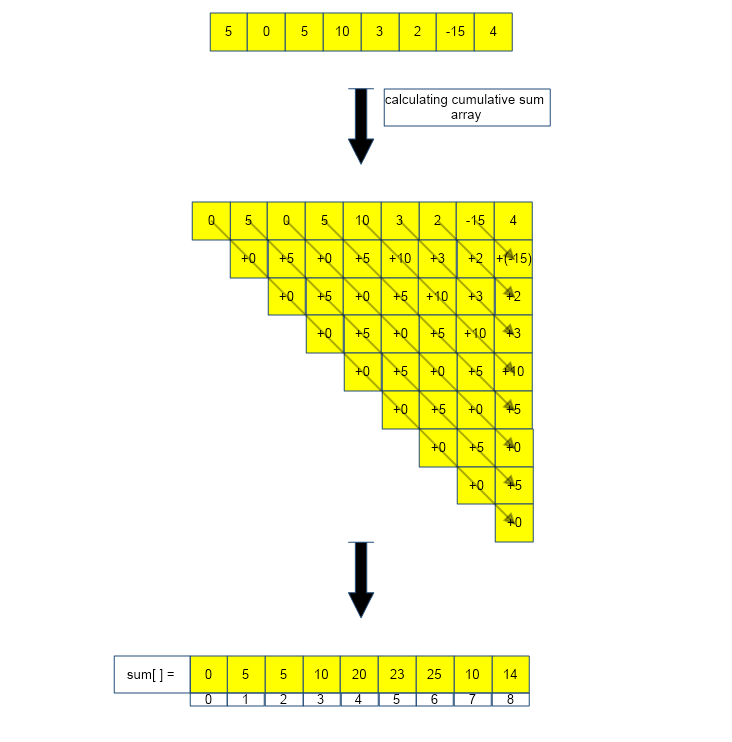


As we observe, there are 7 (count = 7) instances where sum of subarray is 5 (k = 5).
Implementation
C++ Program For Subarray sum equals k
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// function to find number of subarrays with sum = k
int subArraySum(vector <int> arr,int k)
{
int n = arr.size();
int count = 0;
// create an array to store cumulative sum
// initialize the array as 0
int *sum = new int[n+1];
memset(sum,0,sizeof(sum));
// find the cumulative sum for each index of arr[]
for(int i=1;i<=n;i++)
sum[i] =sum[i-1]+arr[i-1];
// generate all the subarrays
// a given subarray within range [start,end]
// is chosen
for(int start=0;start<n;start++)
{
for(int end=start+1;end<=n;end++)
{
// find the sum in range[start,end]
// using sum array (which is used to store cumulative sum)
// if sum equals to given k
// then increase the count
if(sum[end] - sum[start] == k)
count++;
}
}
return count;
}
// main program to implement above functions
int main()
{
vector <int> arr = {5,0,5,10,3,2,-15,4};
int k = 5;
cout<<"Number of subarrays with sum equal to "<<k<<" = "<<subArraySum(arr,k)<<endl;
return 0;
}Output
Number of subarrays with sum equal to 5 = 7
Java Program For Subarray sum equals k
import java.io.*;
import java.util.*;
class tutorialCup
{
// function to find number of subarrays with sum = k
static int subArraySum(ArrayList <Integer> arr,int k)
{
int n = arr.size();
int count = 0;
// create an array to store cumulative sum
// initialize the array as 0
int[] sum = new int[n+1];
sum[0] = 0;
// find the cumulative sum for each index of arr[]
for(int i=1;i<=n;i++)
sum[i] =sum[i-1]+arr.get(i-1);
// generate all the subarrays
// a given subarray within range [start,end]
// is chosen
for(int start=0;start<n;start++)
{
for(int end=start+1;end<=n;end++)
{
// find the sum in range[start,end]
// using sum array (which is used to store cumulative sum)
// if sum equals to given k
// then increase the count
if(sum[end] - sum[start] == k)
count++;
}
}
return count;
}
// main program to implement above functions
public static void main (String[] args)
{
ArrayList <Integer> arr = new ArrayList<Integer>(Arrays.asList(5,0,5,10,3,2,-15,4));
int k = 5;
System.out.println("Number of subarrays with sum equal to "+k+" = "+subArraySum(arr,k));
}
}
Output
Number of subarrays with sum equal to 5 = 7
Complexity Analysis
- Time Complexity : T(n) = O(n2)
- Space Complexity : A(n) = O(n)
Without using extra space
Approach
We can directly find the sum on the go while considering different points.We can choose a particular start point (loop over [0 to n-1]) and iterate over all the elements to it’s right (loop over[start to n-1]) in an inner loop. We keep adding the elements while iterating in the inner loop into sum. Whenever the sum equals the required k value, we increment count. We do so while iterating over all the elements to the right of given start index for every possible start index value.
Algorithm
- Run an outer loop in range[0,n-1]. Loop variable is start.
- create a variable sum to store sum of elements in inner loop and initialize it with 0.
- Run an inner loop in range[start,n-1]. Loop variable is end.
- While iterating in the inner loop find sum of elements up to each value of end.
- While iterating in the inner loop, if value of sum becomes equal to given k,increment the value of count.
- For the next iteration reassign sum as 0.
Implementation
C++ Program For Subarray sum equals k
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// function to find number of subarrays with sum = k
int subArraySum(vector <int> arr,int k)
{
int n = arr.size();
int count = 0;
// start with each element of arr
for (int start = 0;start < n; start++)
{
int sum=0;
// find sum of elements until end
for (int end = start;end < n; end++)
{
sum += arr[end];
// if sum equals to given k
// increment the count
if (sum == k)
count++;
}
}
return count;
}
// main program to implement above functions
int main()
{
vector <int> arr = {5,0,5,10,3,2,-15,4};
int k = 5;
cout<<"Number of subarrays with sum equal to "<<k<<" = "<<subArraySum(arr,k)<<endl;
return 0;
}Output
Number of subarrays with sum equal to 5 = 7
Java Program For Subarray sum equals k
import java.io.*;
import java.util.*;
class tutorialCup
{
// function to find number of subarrays with sum = k
static int subArraySum(ArrayList <Integer> arr,int k)
{
int n = arr.size();
int count = 0;
// start with each element of arr
for (int start = 0;start < n; start++)
{
int sum=0;
// find sum of elements until end
for (int end = start;end < n; end++)
{
sum += arr.get(end);
// if sum equals to given k
// increment the count
if (sum == k)
count++;
}
}
return count;
}
// main program to implement above functions
public static void main (String[] args)
{
ArrayList <Integer> arr = new ArrayList<Integer>(Arrays.asList(5,0,5,10,3,2,-15,4));
int k = 5;
System.out.println("Number of subarrays with sum equal to "+k+" = "+subArraySum(arr,k));
}
}
Output
Number of subarrays with sum equal to 5 = 7
Time Complexity
- Time Complexity : T(n) = O(n2)
- Space Complexity : A(n) = O(1)
Using Hash Map data structure
Approach
As we now understand that if the cumulative sum up to two indices, say i and j is at a difference of k. i.e. if sum[i]−sum[j]=k, then sum of elements lying between indices i and j is k.
We create a hashmap which is used to store the cumulative sum up to all the indices possible along with the number of times the a particular sum value occurs. The required data is stored in map in form map(sum -> number of occurrences of sum in contiguous subarray). We traverse over the array arr[] and keep on finding the cumulative sum and store it in variable sum. Every time we encounter a new sum, we make a new entry in the hashmap corresponding to that sum.
If the same sum occurs again, we increment the count (value for that particular sum in hashmap) corresponding to that sum in the hashmap. Further, for every sum encountered, we also determine the number of times the has occured already(as key value), As it basically determines the number of times a subarray with sum = k has occured upto the current index.So, we have to increment the count by the same amount. At the end of traversal value of count is our required result.
Algorithm
- create a hashmap map.
- Traverse the given array.
- At each step, sum all the elements(find cumulative sum) upto index i, store it in sum.
- check if sum – k is present as key in the map, this done to check whether there exists a subarray ending with i whose sum is equal to k or not.
- if sum – k is present(subarray ending at i with sum = k exists), increment the value of count by mapped value for sum – k in the map.
- don’t forget to add/increase the count of sum (cumulative sum) obtained in each step into the map.
The above algorithm is depicted below :
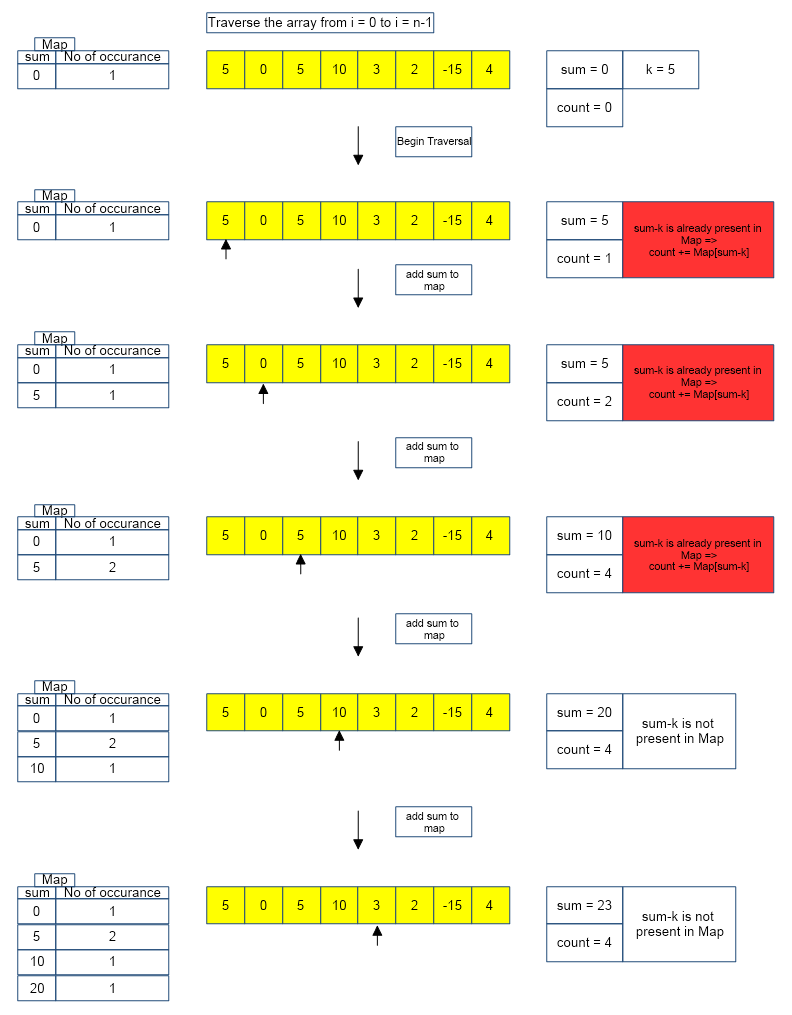
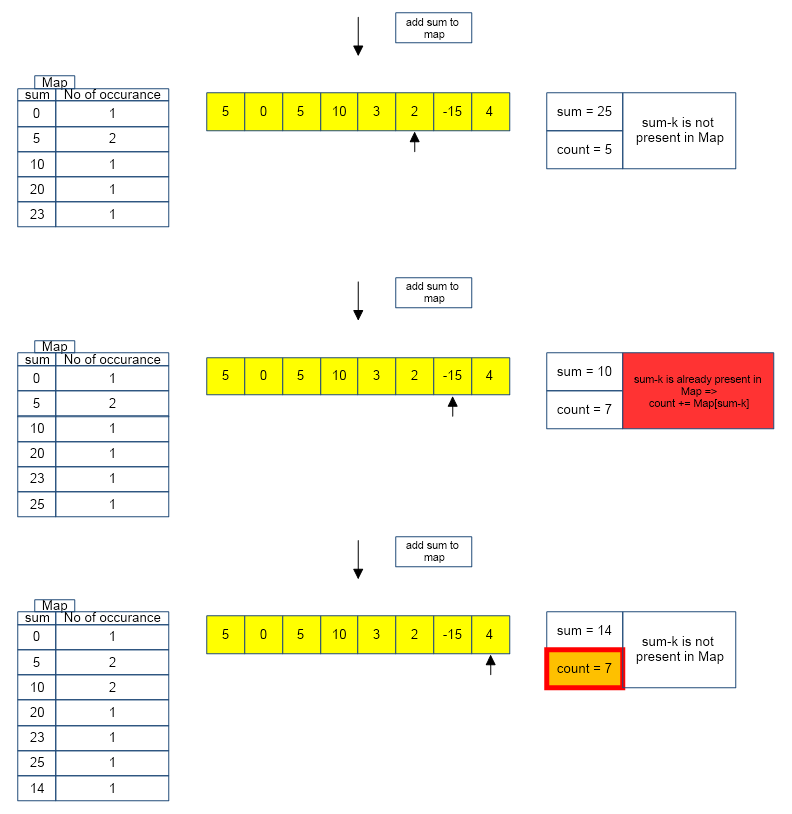
Implementation
C++ Program For Subarray sum equals k
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// function to find number of subarrays with sum = k
int subArraySum(vector <int> arr,int k)
{
int n = arr.size();
int count = 0,sum = 0;
// create a hashmap
unordered_map <int,int> Map;
// when no element is chosen, value of sum is 0
Map[0] = 1;
for (int i = 0; i < n; i++)
{
// in each step, find the cumulative sum
sum += arr[i];
// check if sum-k exists in map
// if exists the increment count by
// mapped value for sum-k
if (Map.find(sum-k) != Map.end())
count += Map[sum-k];
// add the cumulative sum obtained until now into the map
Map[sum] = Map[sum] + 1;
}
return count;
}
// main program to implement above functions
int main()
{
vector <int> arr = {5,0,5,10,3,2,-15,4};
int k = 5;
cout<<"Number of subarrays with sum equal to "<<k<<" = "<<subArraySum(arr,k)<<endl;
return 0;
}Output
Number of subarrays with sum equal to 5 = 7
Java Program For Subarray sum equals k
import java.io.*;
import java.util.*;
class tutorialCup
{
// function to find number of subarrays with sum = k
static int subArraySum(ArrayList <Integer> arr,int k)
{
int n = arr.size();
int count = 0,sum = 0;
// create a hashmap
HashMap <Integer, Integer> map = new HashMap <>();
// when no element is chosen, value of sum is 0
map.put(0, 1);
for (int i = 0; i < n; i++)
{
// in each step, find the cumulative sum
sum += arr.get(i);
// check if sum-k exists in map
// if exists the increment count by
// mapped value for sum-k
if (map.containsKey(sum - k))
count += map.get(sum - k);
// add the cumulative sum obtained until now into the map
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
return count;
}
// main program to implement above functions
public static void main (String[] args)
{
ArrayList <Integer> arr = new ArrayList<Integer>(Arrays.asList(5,0,5,10,3,2,-15,4));
int k = 5;
System.out.println("Number of subarrays with sum equal to "+k+" = "+subArraySum(arr,k));
}
}
Output
Number of subarrays with sum equal to 5 = 7
Complexity Analysis
- Time Complexity : T(n) = O(n)
- Space Complexity : A(n) = O(n)