Pascal Triangle Leetcode

The Pascal Triangle is a very good Leetcode problem that is asked so many times in Amazon, Microsoft, and other companies. we have given non-negative integer rows, print first rows rows of the pascal triangle.

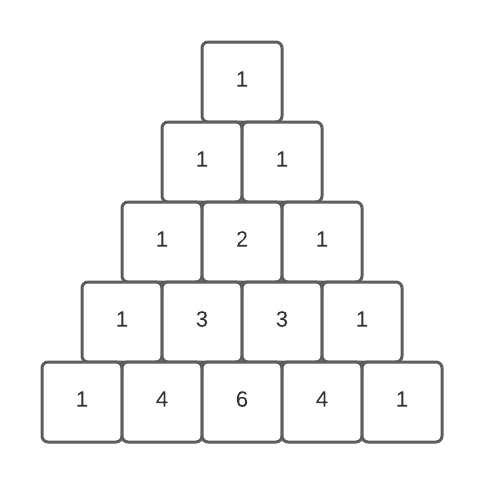
Example

rows = 5

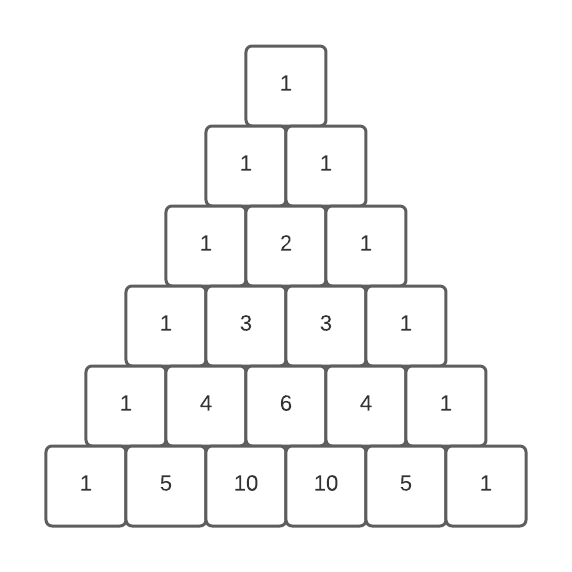
rows = 6

Types of solution for Pascal Triangle Leetcode

1. Dynamic Programming

Dynamic Programming

Approach

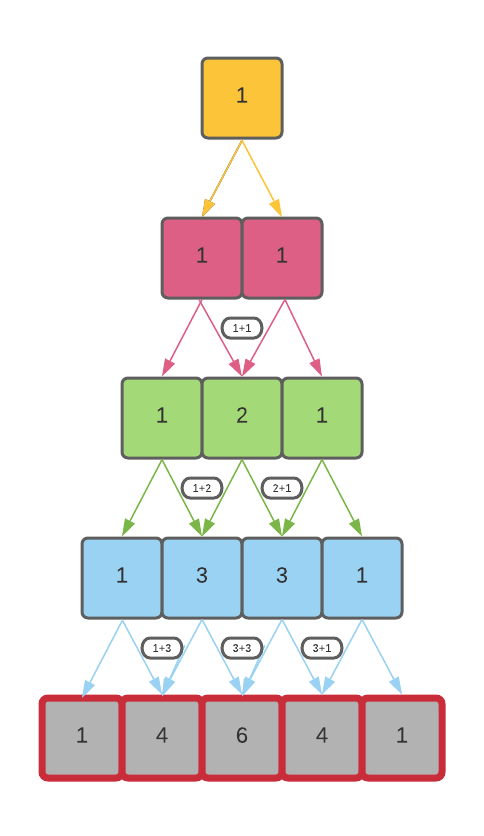
The idea is to understand that if we have a row of pascal triangle, we can easily calculate the next row by iteratively adding adjacent values of the current row. This iterative process of generating a pascal triangle has been considered to be a dynamic programming approach wherein we construct each row based on the previous row.

Algorithm for Pascal Triangle Leetcode

1. define base cases.
2. Initialize the first row of the pascal triangle as {1}.
3. Run an outer loop from i = 0 to i = rows, for generating each row of the triangle.
4. Run an inner loop from j = 1 to j = {previous row size} for calculating element of each row of the triangle.
5. in the inner loop, while calculating the elements of a row, add each pair of adjacent elements of the previous row in each step of the inner loop.
6. After the inner loop gets over, simply output the row generated.
7. Perform the outer loop for the number of rows given and subsequently print each row of the pascal triangle.

The algorithm is depicted below:

Implementation

C++ Program for Pascal Triangle Leetcode

#include <iostream>
#include <bits/stdc++.h>
using namespace std;

void pascalTriangle(int rows)
{
    if(rows == 0)
    return;
    
    vector <int> rowVector;
    
    for(int i=0;i<rows;i++)
    {
        rowVector.insert(rowVector.begin(),1);
        
        for(int j=1;j<rowVector.size() - 1 ;j++)
        rowVector[j] = rowVector[j]+rowVector[j+1];
        
        for(auto i : rowVector)
        cout<<i<<" ";
        
        cout<<endl;
    }
}
int main()
{
    int rows = 5;
    
    cout<<"The pascal triangle of "<<rows<<" rows is"<<endl;
    pascalTriangle(rows);
    
    
    return 0;
}

The pascal triangle of 5 rows is
1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 

Java Program for Pascal Triangle Leetcode

import java.io.*;
import java.util.*;

class TutorialCup
{
    static void pascalTriangle(int rows)
    {
        if(rows == 0)
        return;
        
        ArrayList <Integer> rowVector = new ArrayList<>();
        
        for(int i=0;i<rows;i++)
        {
            rowVector.add(0,1);
            
            for(int j=1;j<rowVector.size() - 1 ;j++)
            rowVector.set(j,rowVector.get(j)+rowVector.get(j+1));
            
            Iterator it = rowVector.iterator();
            
            while(it.hasNext())
                System.out.print((Integer)it.next()+" ");
            
            System.out.println();
        }
    }
    public static void main (String[] args) 
    {
        int rows = 5;
    
        System.out.println("The pascal triangle of "+rows+" rows is");
        pascalTriangle(rows);
    }
}

The pascal triangle of 5 rows is
1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1

Complexity Analysis

1. Time complexity: T(n) = O(rows²), two nested loops.
2. Space complexity: A(n) = O(rows²), for storing each of the rows of the pascal triangle.

References