Tree Traversal (Preorder, Inorder & Postorder)

Difficulty Level Easy
Frequently asked in Adobe Amazon MAQ Oracle Snapdeal
Binary Tree Tree Tree TraversalViews 2261

First, we need to know about what is Traversal in Binary Tree. Traversal is a type of method in which we visit all the nodes exactly once in some specific manner/order. Basically there are two types of traversal in Binary Tree:

We already know about what is the concept of BFS. Now, we see Preorder, Inorder, and Postorder traversal and these traversals are the part of DFS of a binary tree. So, we see all tree type in detail:

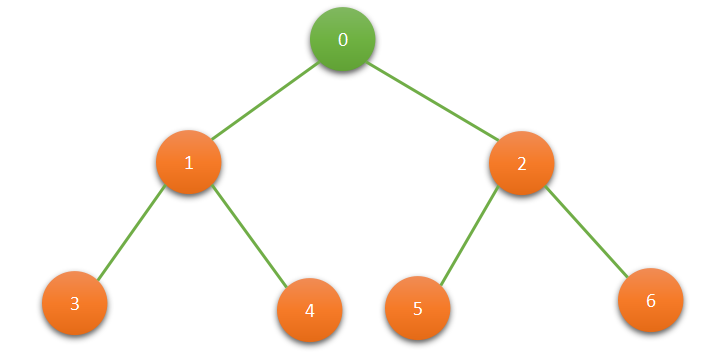
Tree Traversal(Preorder, Inorder & Postorder)

Preorder Traversal

In this traversal, we first print the data of the current node and then move to the left subtree first and after that move to the right subtree. The preorder traversal of the above binary tree is 0 1 3 4 2 5 6.

Algorithm

Algorithm: 
Preorder(root): 
Step:1 Print the data of the Node. 
Step:2 Move to the left side of the node(traverse left-subtree). 
Step:3 Move to the right side of the node(traverse right-subtree).

Inorder Traversal

In this traversal, we first move to the left subtree and then print the data of the node. After printing the data of the node move to the right subtree. The inorder traversal of the above binary tree is 1 3 4 0 2 5 6.

Algorithm

Algorithm:  
Inorder(root): 
Step:1 Move to the left side of the node(traverse left-subtree). 
Step:2 Print the data of the Node.  
Step:3 Move to the right side of the node(traverse right-subtree).

Postorder Traversal

In this traversal, we first move to the left subtree and then move to the right subtree. After moving print the data of the node. The postorder traversal of the above binary tree is 1 3 4 2 5 6 0.

Algorithm

Algorithm: 
Postorder(root): 
Step:1 Move to the left side of the node(traverse left-subtree). 
Step:2 Move to the right side of the node(traverse right-subtree). 
Step:3 Print the data of the Node.

Implementation

/*C++ Implementation of print the Preorder, Inorder, Postorder traversal of given binary tree*/ 
#include<bits/stdc++.h> 
using namespace std; 
/*Structure of Node of BT which contain pointer to left child and right child and a data for node.*/
struct Node{
    int data;
    struct Node* left;// for left child;
    struct Node* right;// for right child;
    Node(int value)// create a node using new Node;
    {
        data=value;
        left=NULL;
        right=NULL;
    }
};
/*Function which print preorder of the given tree*/ 
void Preorder_tree(Node* root)
{
    if(root==NULL)
    {
        return;
    }
    cout<<root->data<<" ";
    Preorder_tree(root->left);
    Preorder_tree(root->right);
}
/*Function which print inorder of the given tree*/ 
void Inorder_tree(Node* root)
{
    if(root==NULL)
    {
        return;
    }
    Preorder_tree(root->left);
    cout<<root->data<<" ";
    Preorder_tree(root->right);
}
/*Function which print postorder of the given tree*/ 
void Postorder_tree(Node* root)
{
    if(root==NULL)
    {
        return;
    }
    Preorder_tree(root->left);
    Preorder_tree(root->right);
    cout<<root->data<<" ";
}
int main() 
{ 
    /*construct tree*/
    Node* root= new Node(0);//root node;
    root->left= new Node(1);
    root->right= new Node(2);
    root->left->left= new Node(3);
    root->left->right= new Node(4);
    root->right->left= new Node(5);
    root->right->right= new Node(6);
    cout<<"Preorder traversal of BT: ";
    Preorder_tree(root);cout<<"\n";
    cout<<"Inorder traversal of BT: ";
    Inorder_tree(root);cout<<"\n";
    cout<<"Postorder traversal of BT: ";
    Postorder_tree(root);cout<<"\n";
    return 0; 
}
Preorder traversal of BT: 0 1 3 4 2 5 6 
Inorder traversal of BT: 1 3 4 0 2 5 6 
Postorder traversal of BT: 1 3 4 2 5 6 0

Time Complexity

O(N) where N is the total number of nodes present in a given binary tree.

References

Translate »