The dividing array into pairs with sum divisible by K is a problem which is asked in interviews with various tweaks now and then. Those who know me know my habit of converting these problems into stories. In this article let us look into this problem.
Table of Contents
Situation To Understand The Problem
With the spread of a pandemic, we have many organizations stepping up to bring in help and relief to the poor. For today we are the coordinator of these relief efforts. We are entrusted with the task of collecting bags of rations and portioning them into “k” bags. The ration we are getting from each household is represented in an array. For a better understanding. Let us look at a sample test-case for more clarity.
Example
Input:
5
A=[4,5,0,-2,-3,1]
Output:
7
The number of subarrays divisible by 5 is:
[4,5,0,-2,-3,1],[5],[5,0],[5,0,-2,-3],[0],[0,-2,-3],[-2,-3]
The array is representing the number of packets we get from each household. We are clubbing together adjacent households for delivering k packets to the nearest location. More easily, we are looking to dividing the array into subarrays that sum to “k”.We can consider various ways to go about the problem. However, in this post, I am presenting the easiest which is very comprehensible.
Algorithm for Dividing Array into Pairs With Sum Divisible by K
- We will be creating an array that is holding the sum up to the said index
- Then we are finding the remainder that we find till this index when the sum is divided by the index
- If the remainder is smaller than 0 we add k
- The Hashmap will be storing the remainder and its occurrence as key-value pairs
- We will then be Finding the number of subsets we can create with each remainder using
- Sum=Sum+value*(value-1)/2
Picture illustrating the process can be
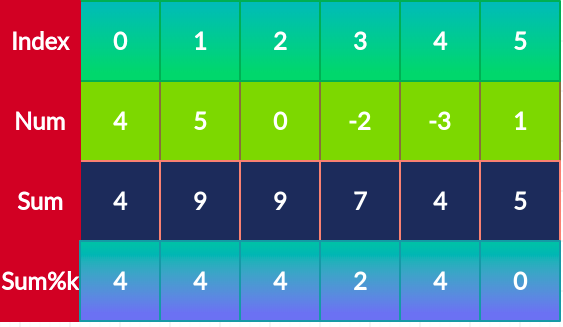
Now that we have a grab of how to do what to do let us look into the code
Java Code
class Solution
{
public int subarraysDivByK(int[] A, int k)
{
if(A==null || A.length<1)
return -1;
int sum[]=new int[A.length+1];
for(int i=1;i<sum.length;i++)
{
sum[i]=sum[i-1]+A[i-1];
}
HashMap<Integer,Integer>combos=new HashMap<Integer,Integer>();
for(int i=0;i<sum.length;i++)
{
int cur=sum[i]%k;
if(cur<0)
cur=cur+k;
if(!combos.containsKey(cur))
combos.put(cur,1);
else
combos.put(cur,combos.get(cur)+1);
}
System.out.println(combos);
int ans=0;
for(int i:combos.values())
{
ans+=i*(i-1)/2;
}
return ans;
}
}C++ Code
class Solution
{
public:
int subarraysDivByK(vector<int>& A, int k)
{
if(A.size()<1)
return -1;
int sum[A.size()+1];
for(int i=1;i<A.size()+1;i++)
{
sum[i]=sum[i-1]+A[i-1];
}
unordered_map<int,int>combos;
for(int i=0;i<A.size()+1;i++)
{
int cur=sum[i]%k;
if(cur<0)
cur=cur+k;
combos[cur]+=1;
}
int ans=0;
for(auto i:combos)
{
ans+=(i.second)*(i.second-1)/2;
}
return ans;
}
};5
{4, 5, 0, -2, -3, 1}7
Complexity Analysis for Dividing Array into Pairs With Sum Divisible by K
In this solution, the time complexity and Space Complexity for the problem can be listed as
Time Complexity=O(n)
Space Complexity=O(n)
How?
Firstly the Space Complexity
- The HashMap consisting of N entries has all the values
- This map is as big as the number of remainders we have with us
- In conclusion, this is leading the space complexity to O(n)
Secondly the Time Complexity
- We are running three loops in the solution
- Firstly, a loop to find the sum=O(n)
- Secondly, a loop to find the remainder=O(n)
- Thirdly finding all the combination=O(remainders)
- In conclusion, all this is leading to time complexity of O(n)