Table of Contents
Problem Statement
“Implementation of Deque using circular array” asks to implement the following functions of a Deque(Doubly Ended Queue) using circular array,
- insertFront(x) : insert an element x at the front of Deque
- insertRear(x) : insert an element x at the rear of Deque
- deleteFront() : delete an element from the front of Deque
- deleteRear() : delete an element from the rear of Deque
- getFront() : return the element present at the front of Deque
- getRear() : return the element present at the rear of Deque
- isEmpty() : return whether or not the Deque is empty
- isFull() : return whether or not the Deque is full
Example
Input
insertFront(5)
insertRear(10)
insertRear(11)
insertFront(19)
getFront()
getRear()
isFull()
deleteRear()
getRear()
deleteFront()
getFront()
isEmpty()
Output
19
11
false
10
5
false
Algorithm for Implementation of Deque using circular array
To implement Deque using a circular array we need to keep track of two pointer front and rear in the array. All the operations will be on these two pointers.
The meaning of circular array can be understood by the image below
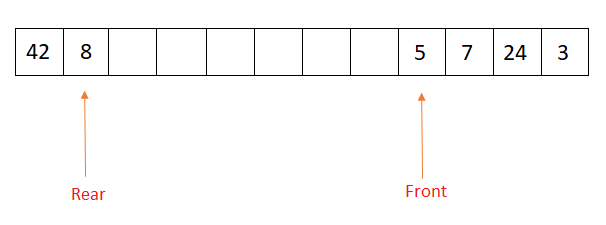
In this image the rear is behind the front, that is when rear was at the end of array and there were some empty slots in the starting of the array, so insertion of an element at the rear would cause the rear to come at position 0, this is because the circular array is circular in nature.
Create an array of size n, where n is the maximum size of Deque and initialize front and rear as -1, before any operation on the Deque.
As the array is circular increment front or rear when they are present at the end of the array will take them to the starting point and similarly decrementing front and rear when they are at the starting point will take them to the end of the array.
insertFront(x)
- If the array is full, the element cannot be inserted.
- If there are no elements in the Deque(or array), that is, front equals -1, increment front and rear, and set arr[front] as x.
- Else decrement front and set arr[front] as x.
Time Complexity = O(1)
insertRear()
- If the array is full, the element cannot be inserted.
- If there are no elements in the Deque, that is, rear equals -1, increment front and rear and set arr[rear] as x.
- Else increment rear and set arr[rear] as x.
Time Complexity = O(1)
deleteFront()
- If the Deque is empty, return.
- If there is only one element in the Deque, that is, front equals rear, set front and rear as -1.
- Else increment front by 1.
Time Complexity = O(1)
deleteRear()
- If the Deque is empty, return.
- If there is only one element in the Deque, that is, rear equals front, set front and rear as -1.
- Else decrement rear by 1.
Time Complexity = O(1)
getFront()
- If the Deque is empty, return.
- Else return arr[front].
Time Complexity = O(1)
getRear()
- If the Deque is empty, return.
- Else return arr[rear].
Time Complexity = O(1)
isEmpty()
If front is equals to -1 the Deque is empty, else it is not.
Time Complexity = O(1)
isFull()
If (rear + 1) % n equals to the front then the Deque is full, else it is not. Here n is the maximum size of Deque.
Time Complexity = O(1)
Java Code for Implementation of Deque using circular array
class ImplementationOfDequeUsingCircularArray {
// Maximum size of Deque
private static final int MAX_SIZE = 100;
// Array to implement Deque
private static int deque[];
// Variables to represent front and rear of dequeue
private static int front = -1;
private static int rear = -1;
private static void insertFront(int x) {
// if array is not full
if (!isFull()) {
// case 1 : there are no elements
// increment front and rear and add element at arr[front]
if (front == -1) {
front = rear = 0;
deque[front] = x;
}
// else, decrement front circularly and add the
// new element at arr[front]
else {
if (front == 0) {
front = MAX_SIZE - 1;
} else {
front--;
}
deque[front] = x;
}
}
}
private static void insertRear(int x) {
// if array is not full
if (!isFull()) {
// if this is the first element to be inserted
// increment front and rear and add element at arr[rear]
if (rear == -1) {
front = rear = 0;
deque[rear] = x;
}
// else increment rear circularly and add
// new element at arr[rear]
else {
if (rear == MAX_SIZE - 1) {
rear = 0;
} else {
rear++;
}
deque[rear] = x;
}
}
}
private static void deleteFront() {
// if array is not empty
if (!isEmpty()) {
// if there is only 1 element
// make front and rear as -1
if (front == rear) {
front = rear = -1;
}
// else increment front circularly
else {
if (front == MAX_SIZE - 1) {
front = 0;
} else {
front++;
}
}
}
}
private static void deleteRear() {
// if array is not empty
if (!isEmpty()) {
// if there is only 1 element
// make front and rear as -1
if (front == rear) {
rear = front = -1;
}
// else decrement rear circularly
else {
if (rear == 0) {
rear = MAX_SIZE - 1;
} else {
rear--;
}
}
}
}
private static int getFront() {
// if array is not empty return arr[front]
if (!isEmpty()) {
return deque[front];
}
return -1;
}
private static int getRear() {
// if array is not empty return arr[rear]
if (!isEmpty()) {
return deque[rear];
}
return -1;
}
private static boolean isEmpty() {
// if front is -1 then deque is empty
if (front == -1) {
return true;
}
return false;
}
private static boolean isFull() {
// if front is 1 ahead of rear then
// deque is full
if ((rear + 1) % MAX_SIZE == front) {
return true;
}
return false;
}
public static void main(String[] args) {
deque = new int[MAX_SIZE];
// Example
insertFront(5);
insertRear(10);
insertRear(11);
insertFront(19);
System.out.println(getFront());
System.out.println(getRear());
System.out.println(isFull());
deleteRear();
System.out.println(getRear());
deleteFront();
System.out.println(getFront());
System.out.println(isEmpty());
}
}19 11 false 10 5 false
C++ Code for Implementation of Deque using circular array
#include <iostream>
using namespace std;
// Maximum size of Deque
const int MAX_SIZE = 100;
// Array to implement Deque
int deque[MAX_SIZE];
// Variables to represent front and rear of dequeue
int front = -1;
int rear = -1;
bool isEmpty() {
// if front is -1 then deque is empty
if (front == -1) {
return true;
}
return false;
}
bool isFull() {
// if front is 1 ahead of rear then
// deque is full
if ((rear + 1) % MAX_SIZE == front) {
return true;
}
return false;
}
void insertFront(int x) {
// if array is not full
if (!isFull()) {
// case 1 : there are no elements
// increment front and rear and add element at arr[front]
if (front == -1) {
front = rear = 0;
deque[front] = x;
}
// else, decrement front circularly and add the
// new element at arr[front]
else {
if (front == 0) {
front = MAX_SIZE - 1;
} else {
front--;
}
deque[front] = x;
}
}
}
void insertRear(int x) {
// if array is not full
if (!isFull()) {
// if this is the first element to be inserted
// increment front and rear and add element at arr[rear]
if (rear == -1) {
front = rear = 0;
deque[rear] = x;
}
// else increment rear circularly and add
// new element at arr[rear]
else {
if (rear == MAX_SIZE - 1) {
rear = 0;
} else {
rear++;
}
deque[rear] = x;
}
}
}
void deleteFront() {
// if array is not empty
if (!isEmpty()) {
// if there is only 1 element
// make front and rear as -1
if (front == rear) {
front = rear = -1;
}
// else increment front circularly
else {
if (front == MAX_SIZE - 1) {
front = 0;
} else {
front++;
}
}
}
}
void deleteRear() {
// if array is not empty
if (!isEmpty()) {
// if there is only 1 element
// make front and rear as -1
if (front == rear) {
front = rear = -1;
}
// else decrement rear circularly
else {
if (rear == 0) {
rear = MAX_SIZE - 1;
} else {
rear--;
}
}
}
}
int getFront() {
// if array is not empty return arr[front]
if (!isEmpty()) {
return deque[front];
}
return -1;
}
int getRear() {
// if array is not empty return arr[rear]
if (!isEmpty()) {
return deque[rear];
}
return -1;
}
int main() {
// Example
insertFront(5);
insertRear(10);
insertRear(11);
insertFront(19);
cout<<getFront()<<endl;
cout<<getRear()<<endl;
if (isFull()) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
deleteRear();
cout<<getRear()<<endl;
deleteFront();
cout<<getFront()<<endl;
if (isEmpty()) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}19 11 false 10 5 false