Find Minimum In Rotated Sorted Array

Problem Statement

“Find Minimum In Rotated Sorted Array” states that you are given a sorted array of size n which is rotated at some index. Find the minimum element in the array.

Example

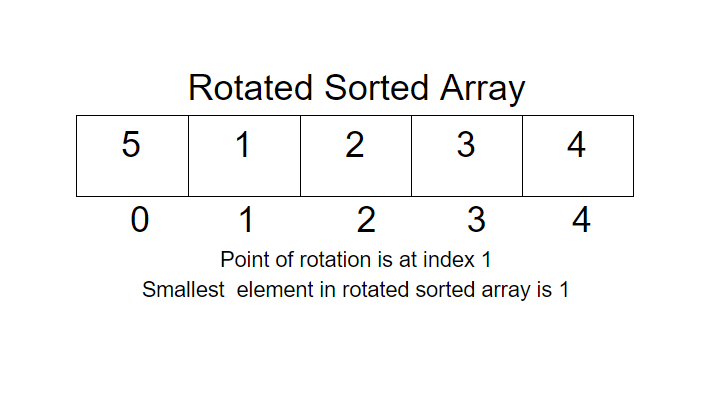
a[ ] = {5, 1, 2, 3, 4}

1

Explanation: If we arrange the array in sorted order it will be [1, 2, 3, 4, 5]. So the smallest number out of all these is 1. And that’s why the output is 1.

a[ ] = {5, 2, 3, 4}

2

Linear Search

Algorithm

1. Initialize a sorted rotated array a[ ] of size n.
2. Create a function to find the minimum in a rotated sorted array which accepts an integer variable as it's a parameter.
3. Initialize an integer variable min as the first element in the given array.
4. Traverse through the given array and check if the element at current index in array a[ ] is less than variable min, update min as current element.
5. Return the integer variable min.

We can use linear search or simply traverse the input array once and find the smallest element in a single traversal. We will simply loop over all the elements in the array and if we find a number which is lesser than our minimum, then we update our answer.

Code

C++ Program to find minimum in rotated sorted array

#include <bits/stdc++.h>
using namespace std;

int findMin(int a[], int n){
    int min = a[0];
    for(int i=1; i<n; i++){
        if(a[i]<min){
            min = a[i];
        }
    }
    return min;
}

int main() {
  int a[] = {5, 2, 3, 4};
  int n = sizeof(a)/sizeof(a[0]);
  cout<<findMin(a, n);
  return 0;
}

2

Java Program to find minimum in rotated sorted array

class MinSearch{
    
    static int findMin(int a[], int n){
        int min = a[0];
        for(int i=1; i<n; i++){
            if(a[i]<min){
                min = a[i];
            }
        }
        return min;
    }
    
  public static void main (String[] args){
    int a[] = {5, 2, 3, 4};
      int n = a.length;
      System.out.println(findMin(a, n));
  }
}

2

Complexity Analysis

Time Complexity

O(N),  because we traversed over all the elements in the array, which has allowed us to achieve a linear time complexity.

Space Complexity

O(1), the algorithm itself takes constant space but the program as a whole takes linear space because of storing the input array.

Binary Search

Algorithm

1. Initialize a sorted rotated array a[ ] of size n.
2. Create a function to find the minimum in a rotated sorted array which accepts an integer variable as it's a parameter.
3. Initialise the three variables beg = 0, end = n-1 and mid = beg+(end-beg)/2.
4. Check if the variable end is less than the variable beg, return a[0].
5. If the variable end is equal to the variable beg, return a[beg].
6. If the variable mid is less than the variable end and a[mid+1] is less than a[mid], return a[mid+1].
7. If mid is greater than beg and a[mid] is less than a[mid+1], return a[mid].
8. If a[end] is greater than a[mid], make a recursive call to function with parameters a, beg, mid-1.
9. Return the recursive call to function itself with the parameters a, mid+1, and end.

The more efficient approach will be to use binary search because the input array is a rotated sorted array. That is the array is sorted but it was rotated at a single point. Since Binary search takes logarithmic time complexity. It’s better to use this solution as compared to the above one.

Code to find minimum in rotated sorted array using binary search

C++ Program

#include <bits/stdc++.h> 
using namespace std; 
  
int findMin(int a[], int beg, int end){  
    if(end < beg) 
        return a[0];  
  
    if(end==beg) 
        return a[beg];  
  
    int mid = beg + (end - beg)/2; 
  
    if(mid<end && a[mid + 1]<a[mid])  
        return a[mid + 1];  
  
    if(mid>beg && a[mid]<a[mid - 1])  
        return a[mid];  
  
    if(a[end]>a[mid])  
    return findMin(a, beg, mid - 1);  
    return findMin(a, mid + 1, end);  
}  
  
int main(){  
    int a[] = {5, 2, 3, 4}; 
    int n = sizeof(a)/sizeof(a[0]);  
    cout<<findMin(a, 0, n-1);  
    return 0;  
}

2

Java Program

class MinSearch{ 
   
    static int findMin(int a[], int beg, int end){ 
        
        if(end < beg) 
            return a[0]; 
            
        if(end==beg) 
            return a[beg];
            
        int mid = beg + (end - beg)/2; 
        
        if(mid<end && a[mid + 1]<a[mid]) 
            return a[mid + 1]; 
        
        if(mid>beg && a[mid]<a[mid - 1]) 
            return a[mid]; 
        
        if(a[end]>a[mid]) 
            return findMin(a, beg, mid - 1); 
        return findMin(a, mid + 1, end); 
    }
        
    public static void main (String[] args){ 
        int a[] = {5, 2, 3, 4}; 
        int n = a.length; 
        System.out.println(findMin(a, 0, n-1)); 
    } 
}

2

Complexity Analysis

Time Complexity

O(log N) where N is the number of elements in the input array. Here we used binary search which takes logarithmic time complexity. All of this possible because the array was initially sorted.

Space Complexity

O(1), this approach takes also constant time but the program as a whole takes O(N) space because of the space required to store the input.