Table of Contents
Problem statement
In the problem ” Largest Perimeter Triangle” we are given an array with n values. All the values are positive integers. Question ask to find the maximum perimeter of the triangle that we can construct from these values. In case it is not possible to construct the triangle then we need to print 0.
Example
arr = [3,2,3,4]
10
Explanation: The largest perimeter of the triangle that can be formed using these values is 10 and the sides of the triangles are 4,3,3.
Approach for Largest Perimeter Triangle Leetcode Solution
This is a basic math problem. So to solve it we must know this theorem that in a triangle sum of the length of any two sides is always greater than the third side. Otherwise, they will not form a triangle. Let us say the sides of the triangle are a,b, and c. The images show how it is not possible to construct a triangle if it does not satisfy this theorem.
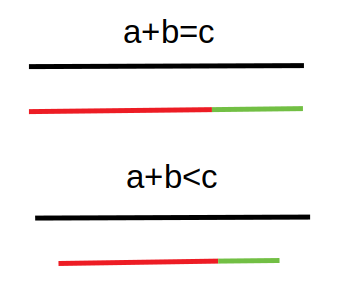
As the question asks to find the largest perimeter triangle, so out of all the possible triplets which satisfy the conditions a+b>c,b+c>a, and a+c>b we need to find the triplet for which a+b+c is maximum.
So we want values of a, b, and c as large as possible to get the largest perimeter. We will sort the array and then we will start with the largest three values if they satisfy the theorem. if it does then their sum is the required value. otherwise, we will check for the next three largest values.
if no such triplet exists then the largest perimeter of the triangle is 0.
Implementation
C++ code for Largest Perimeter Triangle
#include <bits/stdc++.h>
using namespace std;
int largestPerimeter(vector<int>& arr) {
int n=arr.size();
sort(arr.begin(),arr.end());
for (int i =n - 1; i > 1; --i)
if (arr[i] < arr[i - 1] + arr[i - 2])
return arr[i] + arr[i - 1] + arr[i - 2];
return 0;
}
int main()
{
vector<int> arr = { 3,2,3,4 };
cout<<largestPerimeter(arr)<<endl;
return 0;
}10
Java code for Largest Perimeter Triangle
import java.util.Arrays;
public class Tutorialcup {
public static int largestPerimeter(int[] arr) {
Arrays.sort(arr);
int n= arr.length;
for (int i =n - 1; i > 1; --i)
if (arr[i] < arr[i - 1] + arr[i - 2])
return arr[i] + arr[i - 1] + arr[i - 2];
return 0;
}
public static void main(String[] args) {
int [] arr = {3,2,3,4};
int ans= largestPerimeter(arr);
System.out.println(ans);
}
}
10
Complexity Analysis of Largest Perimeter Triangle Leetcode Solution
Time complexity
The time complexity of the above code is O(nlogn) because we are sorting the array. Here n is the size of the array.
Space complexity
The space complexity of the above code is O(1) because we are using only a variable to store the answer.