Check If It Is a Straight Line Leetcode Solution

Difficulty Level Easy
Frequently asked in Palantir Technologies
algorithms Array coding Interview interviewprep LeetCode LeetCodeSolutions MathViews 7509

In this problem, we are given an array of points. This represents a list of x-coordinates and y-coordinates of some points that lie on an X-Y 2-D plane. We need to check if these points form a straight line. Note that there will be at least 2 points in the input and their absolute values will not exceed 10^4.

Example

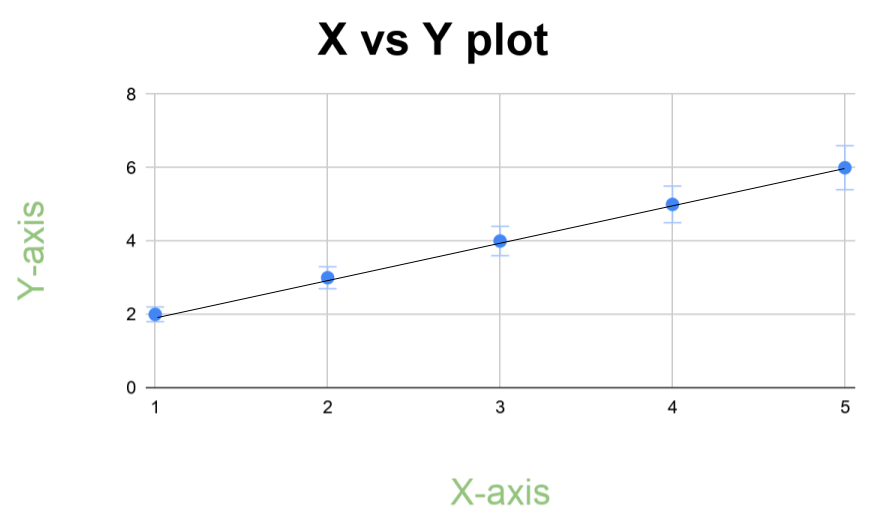
Co-ordinates = {{1 , 2} , {2 , 3} , {3 , 4} , {4 , 5} , {5 , 6}}
true

Explanation The following diagram confirms that all points are collinear.

Check If It Is a Straight Line Leetcode Solution

Co-ordinates = {{1 , 2} , {3 , 4}}
true

Explanation: Two connected points always form a straight line.

Approach

It is easy to observe that if there are only two points in the given list then they will always form a straight line and the result will be true. However, if there are three points, all of them may or may not be collinear. So, we can fix any two points, form a line passing through them, and check if all the other points lie on the same line. Mathematically, this can be done by checking the slope of the line formed between any two points. For example, let us consider we have three points: P1 = (x1 , y1) , P2 = (x2 , y2) and P3 = (x3 , y3).

Now, let’s form a line passing through P1 and P2. The slope of this line will be:

Slope = (y2 – y1) / (x2 – x1)

In order to ensure that P3 is collinear with P1 and P2, let us find the slope of the line formed by points P2 and P3 first. That is,

Slope(P2 and P3) = (y3 – y2) / (x3 – x2)

Now, the points are collinear only and only if: Slope of line formed by P1 and P2 = Slope of line formed by P2 and P3.

Therefore, if P1, P2 and P3 are collinear, we have

(y2 – y1) : (x2 – x1) :: (y3 – y2) : (x3 – x2) , or

(y2 – y1) * (x3 – x2) = (x2 – x1) * (y3 – y2)

Therefore, we can fix two points, say P1 and P2, and for every i > 2 in the input list, we can check if slope(1 , 2) is equal to Slope(1 , i) by cross-product check as we saw above.

Algorithm

  1. We use a boolean function checkStraightLine() to return whether an array of points passed to it forms a straight line
  2. If the array has only 2 points:
    • return true
  3. Initialize x0 as x-coordinate of first point and y0 as y-coordinate of second point. Similarly, (x1 , y1) for coordinates of second point
  4. Since we need their difference for cross-product check, store their differences as:
    • dx = x1 – x0
    • dy = y1 – y0
  5. Now for every point in the array after the second point:
    1. Store x and y coordinates of this point in variables x and y
    2. Now, we check whether the slopes of the first two points and the slope of this and the first point are the same:
      • If dy * (x – x0) is not equal to dx * (y – y0)
        • return false
  6. Return true
  7. Print the result

Implementation of Check If It Is a Straight Line Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;

bool checkStraightLine(vector <vector <int> > &coordinates)
{
    if(coordinates.size() == 2)
        return true;

    int x0 = coordinates[0][0] , x1 = coordinates[1][0];
    int y0 = coordinates[0][1] , y1 = coordinates[1][1];

    int dx = x1 - x0 , dy = y1 - y0;
    for(int i = 2 ; i < coordinates.size() ; i++)
    {
        int x = coordinates[i][0] , y = coordinates[i][1];
        if(dy * (x - x0) != dx * (y - y0))
            return false;
    }
    return true;
}

int main()
{
    vector <vector <int> > coordinates = {{1 , 2} , {2 , 3} , {3 , 4} , {4 , 5} , {5 , 6}};
    cout << (checkStraightLine(coordinates) ? "true\n" : "false\n");
}

Java Program

class check_straight_line
{
    public static void main(String args[])
    {
        int[][] coordinates = {{1 , 2} , {2 , 3} , {3 , 4} , {4 , 5} , {5 , 6}};
        System.out.println(checkStraightLine(coordinates) ? "true" : "false");
    }

    static boolean checkStraightLine(int[][] coordinates)
    {
        if(coordinates.length == 2)
            return true;

        int x0 = coordinates[0][0] , x1 = coordinates[1][0];
        int y0 = coordinates[0][1] , y1 = coordinates[1][1];

        int dx = x1 - x0 , dy = y1 - y0;
        for(int i = 2 ; i < coordinates.length ; i++)
        {
            int x = coordinates[i][0] , y = coordinates[i][1];
            if(dy * (x - x0) != dx * (y - y0))
                return false;
        }
        return true;
    }
}
true

Complexity Analysis of Check If It Is a Straight Line Leetcode Solution

Time Complexity

O(N) where N = number of points in the array. We do a single pass of the array and all the operations performed in it take constant time.

Space Complexity

O(1) as we only use constant memory space.

Translate »