Palindrome Linked List Leetcode Solution

In the problem “Palindrome Linked List”, we have to check whether a given singly integer linked list is a palindrome or not.

Table of Contents

Example

List = {1 -> 2 -> 3 -> 2 -> 1}

true

Explanation #1: The list is palindrome as all elements from the start and back are the same in value.

List = {1 -> 2 -> 3 -> 4 -> 5}

false

Explanation #2: The list is not palindrome as elements from back and forth are not the same.

Approach(Recursion)

This is easy to notice that we need to have the details of the nodes from the back of the array for checking palindrome properties. In this case, we have a singly linked list meaning that we can only iterate forward to reach any node. Thus, it becomes important to use some data structure to hold the nodes from the back, e.g. stack is a possible option as it keeps the most recent node at the top. We can also use recursion similarly. Recursion is an elegant to get the node values in reverse order. Consider the below general pseudocode for better understanding:

inorderTraversal(root)
{
    if(root == null)
        return;
    inorderTraversal(root.left);
    print(root.data);
    inorderTraversal(root.right);
}

The above code first prints left nodes in the tree because we recursively call the function to go to left children of any root before printing the value of the node itself. Similarly, we can use recursion to go to the last nodes first and when the function will backtrack, we will be getting the node values in reverse order. We will use a variable to iterate forward which will be unaffected by recursion. In this way, we can compare forward iterator’s value and reverse node’s value obtained by recursion to compare elements.

Algorithm

A function isPalindrome() is used to return whether a list with head is palindrome or not
We declare a data member of the class named front to store nodes for forward iterations
In isPalindrom():
- Initialize front = head
- return palindromeCheck(head)
In palindromeCheck(current):
- If current is null:
  - return true
- If palindromeCheck(current.next) is false:
  - return false
- If current.value is not equal to front.value
  - return false
- increment front as:
  - front = front.next
- return true as we performed all the checks
Print the result

Implementation of Palindrome Linked List Leetcode Solution

C++ Program

#include <bits/stdc++.h>
using namespace std;
struct listNode
{
    int value;
    listNode* next;
    listNode(int x)
    {
        value = x;
        next = NULL;
    }
};

bool palindromeCheck(listNode* head)
{
    if(head == NULL)
        return true;
    if(!palindromeCheck(head->next))
        return false;
    if(front->value != head->value)
        return false;
    front = front->next;
    return true;
}

bool isPalindrome(listNode* head)
{
    front = head;
    return palindromeCheck(head);
}

int main()
{
    listNode* head = new listNode(1);
    head->next = new listNode(2);
    head->next->next = new listNode(3);
    head->next->next->next = new listNode(2);
    head->next->next->next->next = new listNode(1);

    cout << (isPalindrome(head) ? "true\n" : "false\n");
    return 0;
}

Java Program

class listNode
{
    int value;
    listNode next;
    listNode(int x)
    {
        value = x;
        next = null;
    }
}

class palindrome_linked_list
{
    static listNode front;
    public static void main(String args[])
    {
        listNode head = new listNode(1);
        head.next = new listNode(2);
        head.next.next = new listNode(3);
        head.next.next.next = new listNode(2);
        head.next.next.next.next = new listNode(1);

        System.out.println((isPalindrome(head)) ? "true" : "false");
    }

    static boolean palindromeCheck(listNode head)
    {
        if(head == null)
            return true;
        if(!palindromeCheck(head.next))
            return false;
        if(front.value != head.value)
            return false;
        front = front.next;
        return true;
    }

    static boolean isPalindrome(listNode head)
    {
        front = head;
        return palindromeCheck(head);
    }
}

true

Complexity Analysis of Palindrome Linked List Leetcode Solution

Time Complexity

O(N) as we traverse the list once using recursion. Here, N = number of nodes in the list.

Space Complexity

O(N) as we call a recursive function to check for every node creating N stack frames in the memory.

Approach(Reverse Other Half)

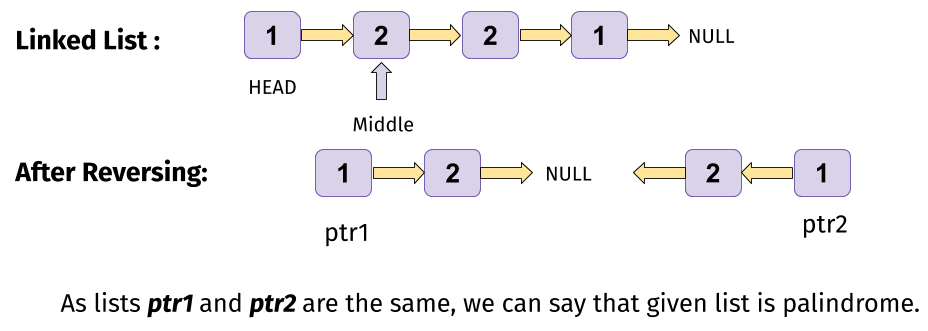
The only way to get rid of the space used in recursion is to modify the given list in-place. We reverse the second half of the linked list and then use two forward iterators for both halves to check if corresponding values are equal. For this process, we need to:

find the middle of the list so that we can reverse the second half.
create a function to reverse the second half of the list
check if the first and second half are equal

All of the above can be done in linear time. After we reverse the linked list, we start checking till the second half gets completed.