Populating Next Right Pointers in Each Node Leetcode Solution

Difficulty Level Medium
Frequently asked in Adobe Amazon Arcesium Bloomberg Facebook Google Microsoft
Binary Tree Breadth First Search Depth First Search Linked-List TreeViews 2632

Problem Statement

The Populating Next Right Pointers in Each Node LeetCode Solution – “Populating Next Right Pointers in Each Node” states that given the root of the perfect binary tree and we need to populate each next pointer of the node to its next right node. If there is no next right node, set the next pointer to null.

Example:

Input:  root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]

Explanation:

Populating Next Right Pointers in Each Node Leetcode Solution

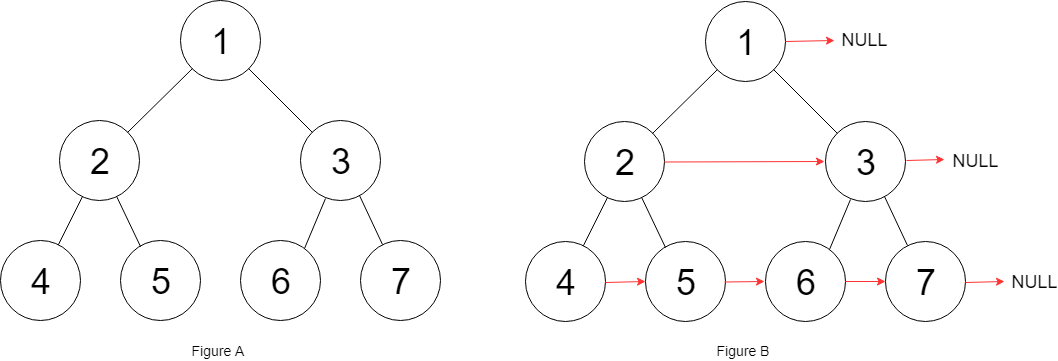
  • Check the above diagram for a better understanding.
Input:  []
Output: []

Explanation:

  • The root is a null pointer, hence [].

Approach

Idea:

  1. The main idea to solve this problem is to use Breadth-First Search.
  2. At each level, store the size of the queue which denotes the number of nodes present at the current level.
  3. Iterate over these nodes and link the node’s next pointers.
  4. Also, push all the nodes to the next level, performing level order traversal.
  5. Return the root of the perfect binary tree after linking the next pointers of each node.

Code

C++ Solution:

class Solution {
public:
    Node* connect(Node* root) {
        if(root==nullptr){
            return root;
        }
        queue<Node*> q;
        q.push(root);
        
        while(!q.empty()){
            int sz = q.size();
            Node* prev = nullptr;
            while(sz--){
                Node* curr = q.front();
                q.pop();
                if(prev!=nullptr){
                    prev->next = curr;
                }
                prev = curr;
                if(curr->left!=nullptr){
                    q.push(curr->left);
                }
                if(curr->right!=nullptr){
                    q.push(curr->right);
                }
            }
        }        
        return root;
    }
};

 Java Solution:

class Solution {
    public Node connect(Node root) {
        if(root == null){
            return null;
        }
        Queue<Node> q = new LinkedList<>();
        q.offer(root);
        while(!q.isEmpty()) {
            Node rightNode = null;
            for(int i = q.size(); i > 0; i--) {
                Node curr = q.poll();
                curr.next = rightNode;
                rightNode = curr;
                if(curr.right != null) {
                    q.offer(curr.right);
                    q.offer(curr.left);
                }
            }
        }
        return root;        
    }
}

Complexity Analysis for Populating Next Right Pointers in Each Node Leetcode Solution

Time Complexity

The time complexity of the above code is O(N) where N = a total number of nodes since we are accessing each node at most 2 times.

Space Complexity

The space complexity of the above code is O(N) since Queue is used to perform a breadth-first search of the above perfect binary tree.

Translate »