Breadth First Search (BFS) for a Graph

Breadth First Search (BFS) for a graph is a traversing or searching algorithm in tree/graph data structure. It starts at a given vertex(any arbitrary vertex) and explores all the connected vertex and after that moves to the nearest vertex and explores all the unexplored nodes and takes care that no vertex/nodes visited twice. To find out the BFS of a given graph starting from a particular node we need a Queue data structure to find out. Let’s move to the example for a quick understanding of the

Table of Contents

Breadth First Search (BFS) traversal and its implementation

When we add connected nodes to a particular node then we also add that node to the result and pop that from the queue for more understanding just see the below step by step procedure:

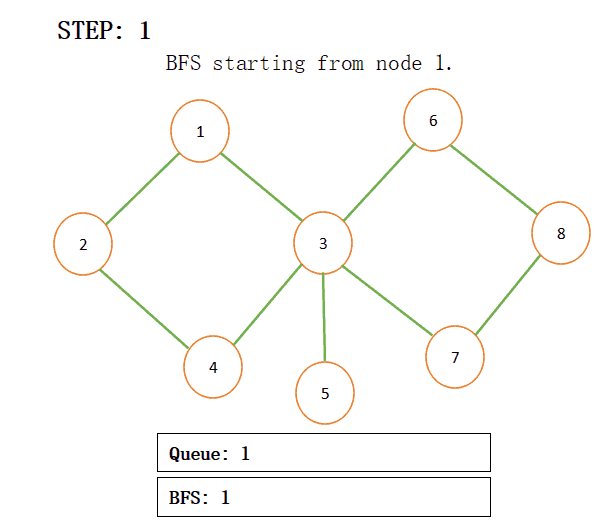
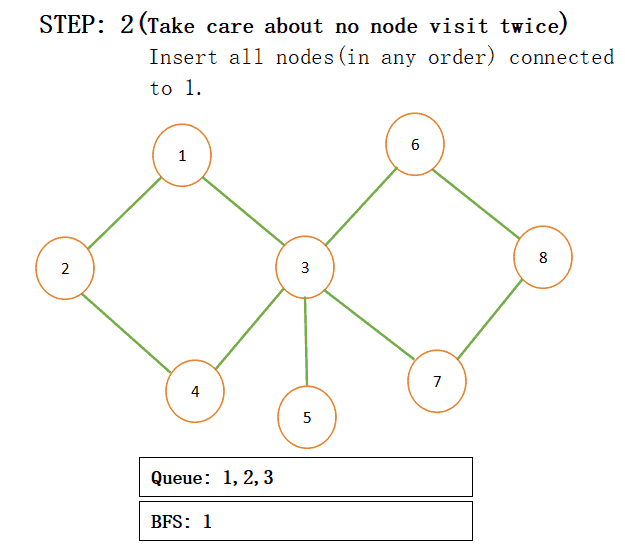
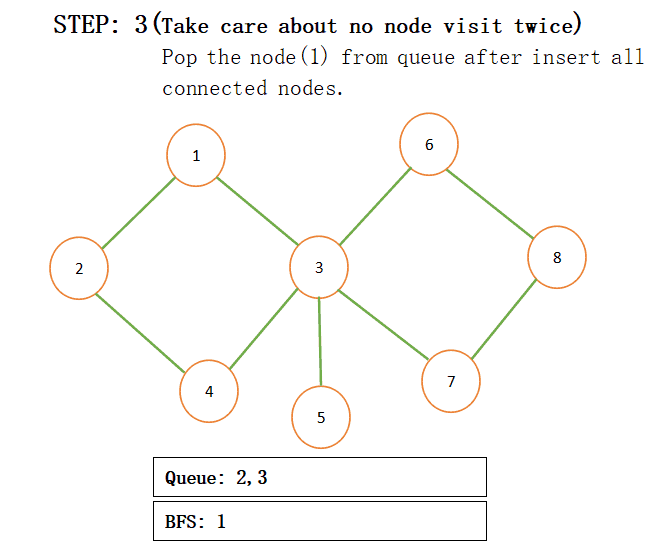
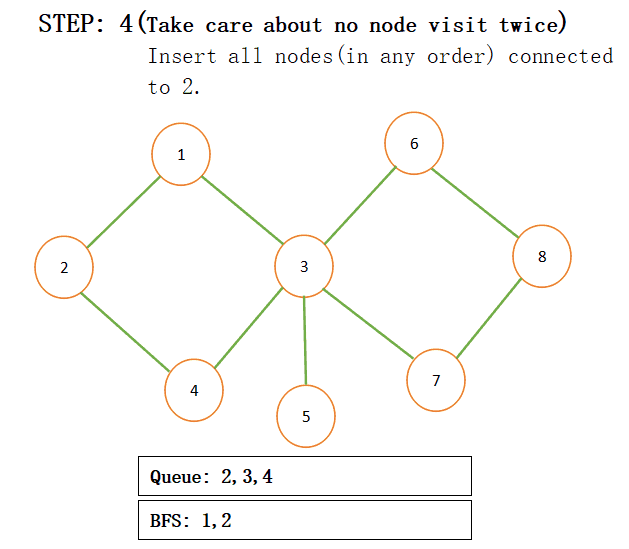
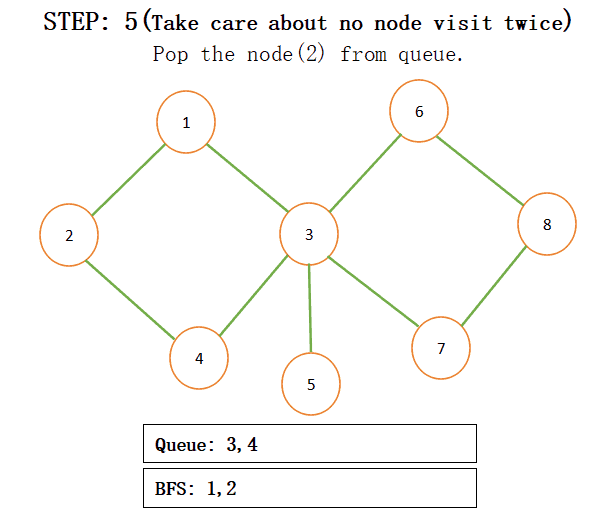
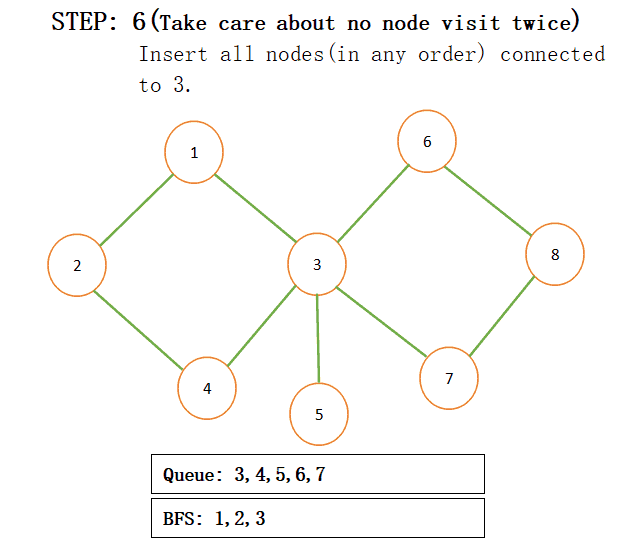
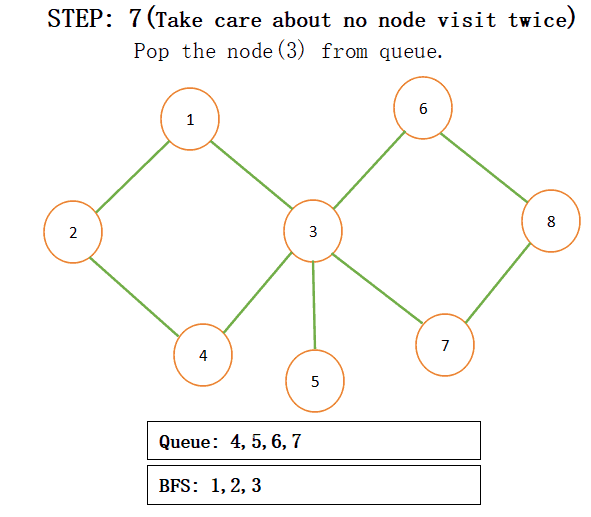
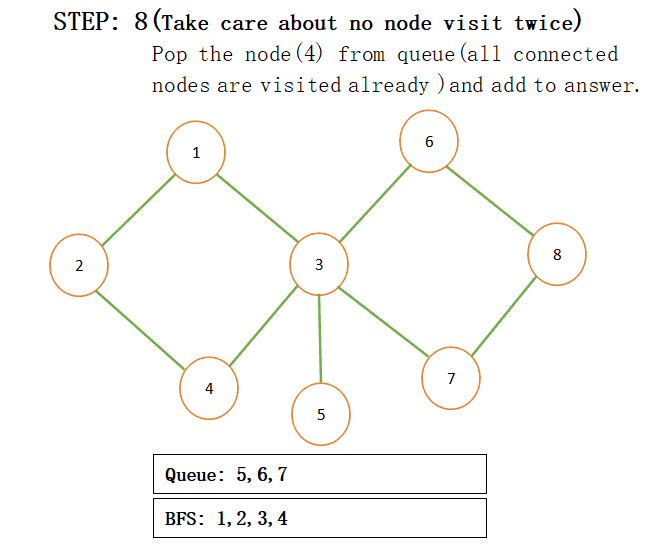
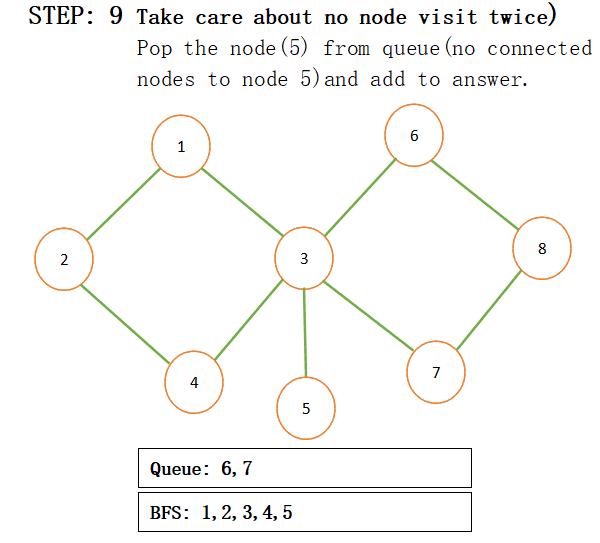
NOTE:

There is more than one BFS possible for a particular graph(like the above graph ). Like some other possible BFS for the above graph are : (1,3,2,5,6,7,4,8) , (1,3,2,7,6,5,4,8), (1,3,2,6,7,5,4,8)….
BFS is level order traversal.

Implementation of Breadth First Search (BFS)

C++ Code for Breadth First Search (BFS)

/*C++ Implementation of BFS of a given graph using STL*/
#include <bits/stdc++.h>
using namespace std;
int main() {
    int nodes,edges;
    /*take input*/
    cin>>nodes>>edges;
    vector<int> v[nodes+1];
    bool visited[nodes+1];
    memset(visited,false,sizeof(visited));
    /*Make graph using vector*/
    for(int i=0;i<edges;i++)
    {
        int x,y;
        cin>>x>>y;
        /*add edge between x and y*/
        v[x].push_back(y);
        /*add edge between y and x*/
        v[y].push_back(x);
    }
    int start;
    /*Take input node at which the BFS starts*/
    cin>>start;
    queue<int> q_calc;
    q_calc.push(start);
    visited[start]=true;
    vector<int> bfs;
    while(!q_calc.empty())
    {
        /*pop the element from queue*/
        int pop_elem=q_calc.front();
        /*update the answer*/  
        bfs.push_back(pop_elem);
        q_calc.pop();
        /*add all the connected nodes with pop_elem into queue*/
        for(int i=0;i<v[pop_elem].size();i++)
        {
            /*if we visit already then we can't add it into queue*/
            if(!visited[v[pop_elem][i]])
            {
                visited[v[pop_elem][i]]=true;
                q_calc.push(v[pop_elem][i]);
            }
        }
    }
    /*print the BFS for given graph at starting with given node*/
    for(int i=0;i<nodes;i++)
    {
        cout<<bfs[i]<<" ";
    }
    cout<<"\n";
  return 0;
}

Output:
1 2 3 4 5 6 7 8

Time Complexity of BFS

O(V+E) where V denotes the number of vertices and E denotes the number of edges.

Reference

Interview Questions