Table of Contents
Problem Statement:
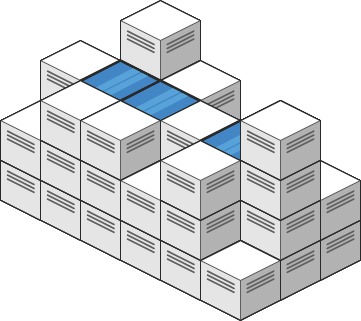
Trapping Rain Water II LeetCode Solution : Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.
Examples:
Input:
heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output:
4
Explanation:
After the rain, water is trapped between the blocks. We have two small ponds 1 and 3 units trapped. The total volume of water trapped is 4.
Approach:
Idea:
The idea is to consider all the boundary cells and then slowly cover the entire matrix with the help of BFS. One thing to remember is that the boundary cells can not store any amount of water in them. The idea is using Priority Queue (implemented with Min Heap) to polling out the node with minimum value. Then applying BFS algorithm to traverse through neighbor nodes.
While doing BFS we will check if the internal cells can store some amount of water in them.
First, we add all the boundary cells into a min-heap and then for each element i inside the min heap we do a BFS to its neighboring cells and calculate what amount of water they can store without the water getting spill out, by taking the ith element as the limiting boundary.
Code:
Trapping Rain Water II C++ Solution:
class Solution {
public:
int trapRainWater(vector<vector<int>>& heightMap) {
priority_queue<vector<int>> minHeap;
int m = heightMap.size();
int n = heightMap[0].size();
vector<vector<bool>> vis(m,vector<bool>(n,false));
for(int i=0;i<n;i++){
minHeap.push({-heightMap[0][i],0,i});
minHeap.push({-heightMap[m-1][i],m-1,i});
vis[0][i] = true;
vis[m-1][i] = true;
}
for(int i=1;i<m-1;i++){
minHeap.push({-heightMap[i][0],i,0});
minHeap.push({-heightMap[i][n-1],i,n-1});
vis[i][0] = true;
vis[i][n-1] = true;
}
int ans = 0;
vector<vector<int>> dirs = {{0,1},{1,0},{0,-1},{-1,0}};
while(!minHeap.empty()){
vector<int> top = minHeap.top();
minHeap.pop();
for(auto it:dirs){
int x = it[0] + top[1];
int y = it[1] + top[2];
if(x>=0 and y>=0 and x<m and y<n and (not vis[x][y])){
vis[x][y] = true;
if(heightMap[x][y] < heightMap[top[1]][top[2]]){
ans += heightMap[top[1]][top[2]] - heightMap[x][y];
heightMap[x][y] = heightMap[top[1]][top[2]];
minHeap.push({-heightMap[x][y],x,y});
}
else{
minHeap.push({-heightMap[x][y],x,y});
}
}
}
}
return ans;
}
};
Complexity Analysis of Trapping Rain Water II LeetCode Solution:
- Time Complexity: The time complexity of the above code is O(nmlog(nm)).
- Space Complexity: The space complexity of the above code is O(nm).