Given a directed acyclic graph, topologically sort the graph nodes.
Table of Contents
Topological Sorting Example

Topological sorting of above graph is -> {1,2,3,0,5,4}
Theory
- Topological Sorting is done for a Directed Acyclic Graph (DAG).
- A DAG has no cycles in it. ie, there is no such path starting from any node of the graph that comes back to that node.
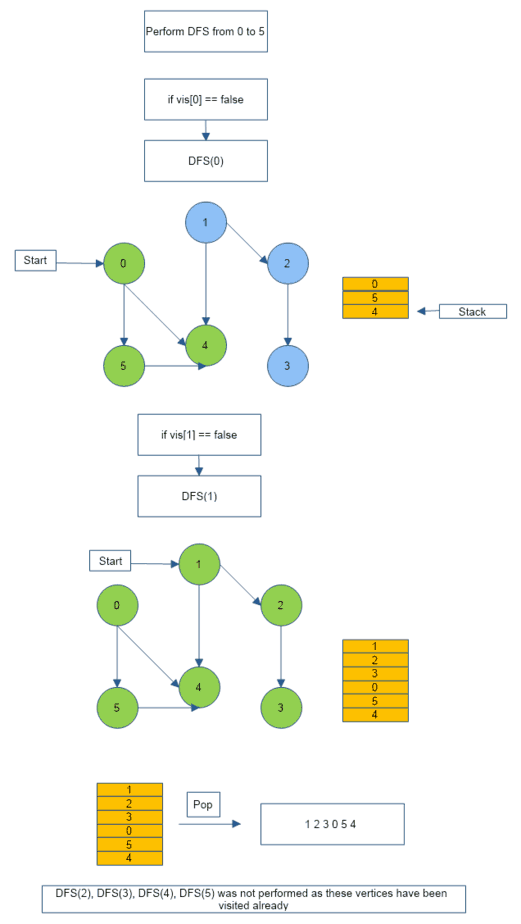
Topological Sorting Algorithm
- We perform Depth First Search (DFS) for an unvisited node (source node) and visit all it’s neighbors recursively in a depth-first manner.
- We mark each neighbor encountered in the path as visited.
- Once we reach the last node (the node from which has no unvisited neighbor), we backtrack, push each node encountered in the path while backtracking into a stack.
- The first node pushed into the stack is the last node visited in DFS traversal.
- The last node pushed into the stack is the first node visited during traversal.
Functions used
- DFS() – perform DFS traversal from a source node.
- topSort() – perform DFS traversal for every unvisited node.

C++ Program
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
// add edge in a directed graph
void add(vector <int> list[],int u,int v)
{
adj[u].push_back(v);
}
// perfrom DFS from source node s
void DFS(int s,vector <int> list[],bool *vis,stack <int> &st)
{
vis[s] = true;
for(auto i : list[s])
{
// visit a node only if unvisited
if(!vis[i])
DFS(i,list,vis,st);
}
// push node into stack while backtracking
st.push(s);
}
void topSort(vector <int> list[],int n)
{
bool *vis = new vis[n];
stack <int> st;
// before performing DFS, mark every node as not visited
for(int i=0;i<n;i++)
vis[i] = false;
// perfrom DFS from every unvisited node
for(int s=0;s<n;s++)
if(!vis[s])
DFS(s,list,vis,st);
// pop the content of the stack
// the order of the elements is order in which tasks are to be performed
while(!st.empty())
{
cout<<st.top()<<" ";
st.pop();
}
}
int main()
{
int n = 6;
vector <int> list[n];
add(list, 0, 5);
add(list, 0, 4);
add(list, 5, 4);
add(list, 1, 4);
add(list, 1, 2);
add(list, 2, 3);
cout <<"Topologically Sorted Graph : ";
topSort(list,n)
return 0;
}Output
Topologically Sorted Graph : 1 2 3 0 5 4
Java Program
import java.io.*;
import java.util.*;
class graph
{
private int v;
private ArrayList<ArrayList<Integer>> adj;
// constructor to generate adjacency list
graph(int n)
{
v = n;
adj = new ArrayList<ArrayList<Integer>> (v);
for(int i=0;i<v;i++)
{
adj.add(new ArrayList<Integer>());
}
}
// add edge in a directed graph
void add(int u,int v)
{
adj.get(u).add(v);
}
// perfrom DFS from source node s
void DFS(int s,boolean vis[],Stack <Integer> st)
{
vis[s] = true;
Integer i;
Iterator <Integer> itr = adj.get(s).iterator();
while(itr.hasNext())
{
i = itr.next();
// visit a node only if unvisited
if(vis[i] == false)
DFS(i,vis,st);
}
// push node into stack while backtracking
st.push(s);
}
void topSort()
{
Stack <Integer> st = new Stack<Integer>();
boolean vis[] = new boolean[v];
// before performing DFS, mark every node as not visited
for(int i=0;i<v;i++)
vis[i] = false;
// perfrom DFS from every unvisited node
for (int i = 0; i < v; i++)
{
if (vis[i] == false)
DFS(i, vis, st);
}
// pop the contents of the stack
// the order of the elements is order in which tasks are to be performed
while (st.empty() == false)
System.out.print(st.pop() + " ");
}
public static void main(String args[])
{
int n = 6;
graph g = new graph(n);
g.add(0, 5);
g.add(0, 4);
g.add(5, 4);
g.add(1, 4);
g.add(1, 2);
g.add(2, 3);
System.out.println("Topologically Sorted Graph :");
g.topSort();
}
}Output
Topologically Sorted Graph : 1 2 3 0 5 4
Complexity Analysis
- Time Complexity: T(n) = O(V+E)
- Space Complexity: A(n) = O(V), stack used for storing vertices
Supplementary Information
- Topological Sorting is applied in job scheduling in computer science, a set of jobs which are interdependent can be put in a certain order for them to be executed.
- In the above example if each node is a job (having the same numbering as the node), then Job 0 and Job 1 are executed before the execution of Job 4.