Insertion Sort

Sort a given unsorted array using the insertion sort algorithm.

Input: {9,5,1,6,11,8,4}

Output: {1,4,5,6,8,9,11}

Theory

• Insertion Sort sorts numbers in the same way as we humans sort a set of numbered objects (ex cards)
• A number is taken from an unsorted array (right subarray) to a position in the sorted array (left subarray) such that the left subarray remains sorted.
• It is an incremental approach-based method.

Insertion Sort Algorithm

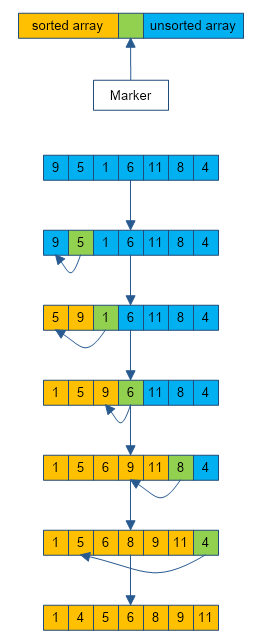
1. Select/Mark the first element in an unsorted array, move it to the correct position in the sorted array.
2. Advance the marker to the next element in an unsorted array.

C++ Program

#include <iostream>
using namespace std;

void insertSort(int arr[],int n)
{
    int i,j,save;

    for(int i=1;i<n;i++)
    {
        j = i-1;
        save = arr[i];
        
        // look for correct position of arr[i]
        while(j>=0 && arr[j] > save)
        {
            // shifting array elements towards the right
            arr[j+1] = arr[j];
            j--;
        }
        // place arr[i] at the correct position
        arr[j+1] = save;
    }
}

int main()
{
    
    int arr[] = {9,5,1,6,11,8,4};
    int n = sizeof(arr)/sizeof(arr[0]);

    insertSort(arr,n);

    for(int i=0;i<n;i++)
    cout<<arr[i]<<" ";
    
    return 0;
}

Output

1 4 5 6 8 9 11

Java Program

class iSort
{
    static void insertSort(int arr[])
    {
        int n = arr.length;
        int i,j,save;

        for(i=1;i<n;i++)
        {
            j = i-1;
            save = arr[i];

            // look for correct position of arr[i]
            while(j >= 0 && arr[j] > save)
            {
                // shifting array elements towards the right
                arr[j+1] = arr[j];
                j--;
            }
            // place arr[i] at the correct position
            arr[j+1] = save;
        }
    }

    public static void main(String args[]) 
    {
        int arr[] = {9,5,1,6,11,8,4};
        insertSort(arr);

        for(int i=0;i<arr.length;i++)
        System.out.print(arr[i] +" ");   
    }
}

Output

1 4 5 6 8 9 11

Complexity Analysis

• Time Complexity: T(n) = O(n²)
• It takes O(n²) time when an array is reversely sorted and O(n) time when the array is sorted.
• Space Complexity: A(n) = O(1)

Supplementary Information

• Insertion Sort is an in-place sorting algorithm.
• It is a stable nature.
• Insertion Sort is useful when the input array is almost sorted, only a few elements are misplaced incomplete big array.
• It is also useful when the array to be sorted is smaller in size.

Reference  Interview Questions