Given the root of a binary search tree and two nodes n1 and n2, find the LCA(Lowest Common Ancestor) of the nodes in a given binary search tree.
Table of Contents
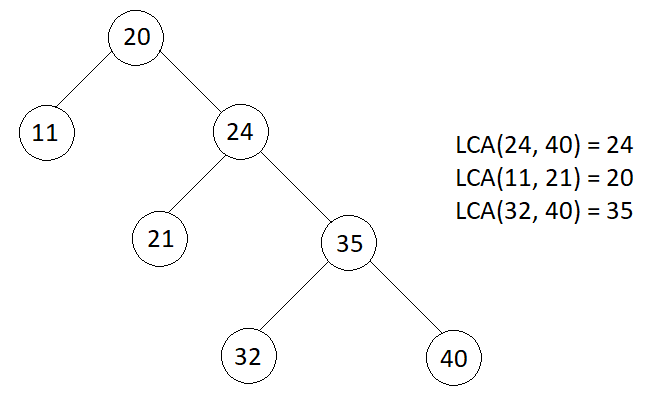
Example
Naive Approach for Lowest Common Ancestor in Binary Search Tree
Find the LCA(n1, n2) using the optimal approach to find LCA in the Binary tree, as BST is also a binary tree.
If we assume that n1 and n2, for which we have to find LCA, exists in the tree, then the above problem can be solved in a single traversal.
Traverse the tree, for every node we have one of the four cases,
- The current node is either n1 or n2, in this case, we return the node.
- One of the subtrees of the current node contains n1 and the other contains n2, this node is the LCA, return the node.
- One subtree of the current node contains both n1 and n2, we return what the subtree returns.
- None of the subtrees contains n1 and n2, return null.
Time Complexity = O(n), with single traversal
where n is the number of nodes in the tree.
Optimal Approach for Lowest Common Ancestor in Binary Search Tree
Using the properties of BST, the LCA can be found in much lesser time complexity.
- Traverse the BST starting from the root (Initialize curr as root).
- If the current node’s value lies between n1 and n2(both inclusive), then this is the LCA.
- Else if node’s value is less than both n1 and n2, LCA is present in the right half (curr becomes curr.right).
- Else LCA is present in the left half (curr becomes curr.left).
Explanation
Consider the BST in the above image, lets find the LCA(32, 40)
Start traversing the tree starting from the root.
- Current node’s value = 20
20 < 32 and 20 < 40, LCA is present in right sub tree - Current node’s value = 24
24 < 32 and 20 < 40, LCA is present in right sub tre - Current node’s value = 35
35 >= 32 and 35 <= 40, so this is the LCA
That is, LCA(32, 40) = 35
JAVA Code for Lowest Common Ancestor in Binary Search Tree
public class LCABST {
// Class to represent a node in BST
static class Node {
int data;
Node left, right;
public Node(int data) {
this.data = data;
left = right = null;
}
}
// Function to return LCA of two nodes, and return -1 if LCA does not exist
private static int LCA(Node root, int n1, int n2) {
// No LCA for an empty tree
if (root == null) {
return -1;
}
// Traverse the tree starting from root
Node curr = root;
int lca = -1;
while (curr != null) {
if (curr.data < n1 && curr.data < n2) {
// LCA is present in the right sub tree
curr = curr.right;
} else if (curr.data > n1 && curr.data > n2) {
// LCA is present in left sub tree
curr = curr.left;
} else {
lca = curr.data;
break;
}
}
// Return LCA
return lca;
}
public static void main(String[] args) {
// Constructing the BST in above example
Node root = new Node(20);
root.left = new Node(11);
root.right = new Node(24);
root.right.left = new Node(21);
root.right.right = new Node(35);
root.right.right.left = new Node(32);
root.right.right.right = new Node(40);
// Queries
System.out.println(LCA(root, 24, 40));
System.out.println(LCA(root, 11, 21));
System.out.println(LCA(root, 32, 40));
}
}C++ Code for Lowest Common Ancestor in Binary Search Tree
#include <iostream>
using namespace std;
// Class representing node of binary search tree
class Node {
public:
int data;
Node *left;
Node *right;
};
// Function to allocate new memory to a tree node
Node* newNode(int data) {
Node *node = new Node();
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// Function to return LCA of two nodes, and return -1 if LCA does not exist
int LCA(Node *root, int n1, int n2) {
// No LCA for an empty tree
if (root == NULL) {
return -1;
}
// Traverse the tree starting from root
Node *curr = root;
int lca = -1;
while (curr != NULL) {
if (curr->data < n1 && curr->data < n2) {
// LCA is present in the right sub tree
curr = curr->right;
} else if (curr->data > n1 && curr->data > n2) {
// LCA is present in left sub tree
curr = curr->left;
} else {
lca = curr->data;
break;
}
}
// Return LCA
return lca;
}
int main() {
// Construct the tree shown in above example
Node *root = newNode(20);
root->left = newNode(11);
root->right = newNode(24);
root->right->left = newNode(21);
root->right->right = newNode(35);
root->right->right->left = newNode(32);
root->right->right->right = newNode(40);
// Queries
cout<<LCA(root, 24, 40)<<endl;
cout<<LCA(root, 11, 21)<<endl;
cout<<LCA(root, 32, 40)<<endl;
return 0;
}24 20 35
Complexity Analysis
Time Complexity = O(h), where h is the height of BST