Given a sorted array(in ascending order), check if the array can be split into 1 or more subsequences of length greater than equals to 3 such that every subsequence contains consecutive numbers.
Table of Contents
Examples
Input:
arr[] = {1,2,3,3,4,5}
Output:
true
Explanation:
The array can be split into 2 subsequences as,
sub1[] = {1, 2, 3}
sub2[] = {3, 4, 5}
Input:
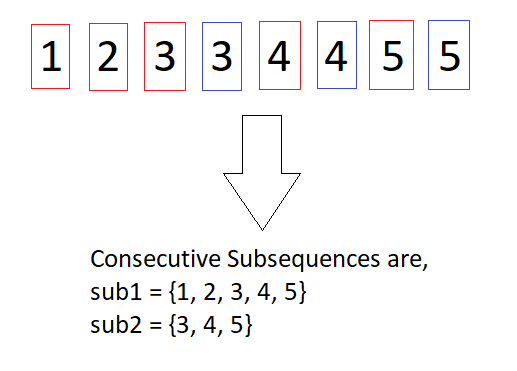
arr[] = {Z1, 2, 3, 3, 4, 4, 5, 5}
Output:
true
Explanation:
The consecutive subsequences are,
sub1[] = {1, 2, 3, 4, 5}
sub2[] = {3, 4, 5}
Naive Approach for Split Array Into Consecutive Subsequences
For an element arr[i] of the given array, it can either form a new subsequence or can be added to a subsequence ending at (arr[i] – 1).
It is always better not to form a new subsequence as forming a new subsequence may result in some subsequences of length less than three. If there is no subsequence ending at (arr[i] – 1), there is no option but to form a new subsequence.
If there are more than one subsequences that can accommodate the current element, always add the current element to the subsequence with the least number of elements, this will ensure the minimization of subsequences of length less than 3.
Algorithm
- The first element of the array always forms a new subsequence.
- Traverse the array starting from index 1(0 based indexing).
- Check if there is some subsequence that can accommodate the current element, an element arr[i] can be added to a subsequence ending at (arr[i] – 1).
- If there is no subsequence that can accommodate the current element form a new subsequence.
- Else choose the subsequence with a minimum size that can accommodate the current element and add the current element to the chosen subsequence.
- After traversing the array, check if there is some subsequence of length less than 3, if yes, return false, else return true.
JAVA Code for Split Array Into Consecutive Subsequences
import java.util.ArrayList;
public class SplitTheArrayIntoConsecutievSubsequences {
private static boolean isPossible(int[] arr) {
// If the lenght of arr is less than 3, it is not possible to split the array
if (arr == null || arr.length < 3) {
return false;
}
int n = arr.length;
// List of subsequences
ArrayList<ArrayList<Integer>> al = new ArrayList<>();
// First element always forms a new subsequence
ArrayList<Integer> eles = new ArrayList<Integer>();
eles.add(arr[0]);
al.add(eles);
// Traverse the array starting from index 1
for (int i = 1; i < n; i++) {
// Required position of subsequence that can accommodate the current element
int pos = -1;
// Size of required subsequence
int size = -1;
// Check if there is some subsequence that can accommodate the current element
for (int j = 0; j < al.size(); j++) {
// A subsequence ending at (arr[i] - 1) can accommodate the element arr[i]
if (al.get(j).get(al.get(j).size() - 1) + 1 == arr[i]) {
if (pos == -1) {
pos = j;
size = al.get(j).size();
} else {
// Select the subsequence with minimum size
if (al.get(j).size() < size) {
pos = j;
size = al.get(j).size();
}
}
}
}
// If there is no subsequence that can accommodate the current element
// form a new subsequence
if (pos == -1) {
ArrayList<Integer> newAL = new ArrayList<>();
newAL.add(arr[i]);
al.add(newAL);
} else {
// else add it to the required subsequence
al.get(pos).add(arr[i]);
}
}
for (int i = 0; i < al.size(); i++) {
// if there is some subsequence of length less than 3, return false
if (al.get(i).size() < 3) {
return false;
}
}
// No subsequence of length less than 3, return true
return true;
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{1, 2, 3, 3, 4, 5};
System.out.println(isPossible(arr1));
// Example 2
int arr2[] = new int[]{1, 2, 3, 3, 4, 4, 5, 5};
System.out.println(isPossible(arr2));
// Example 3
int arr3[] = new int[]{1, 2, 3, 4, 4, 5};
System.out.println(isPossible(arr3));
}
}true true false
C++ Code for Split Array Into Consecutive Subsequences
#include<bits/stdc++.h>
using namespace std;
bool isPossible(int *arr, int n) {
if (n < 3) {
return false;
}
// List of subsequences
vector<vector<int>> v;
// First element always forms a new subsequence
vector<int> eles;
eles.push_back(arr[0]);
v.push_back(eles);
// Traverse the array starting from index 1
for (int i = 1; i < n; i++) {
// Required position of subsequence that can accommodate the current element
int pos = -1;
// Size of required subsequence
int size = -1;
// Check if there is some subsequence that can accommodate the current element
for (int j = 0; j < v.size(); j++) {
// A subsequence ending at (arr[i] - 1) can accommodate the element arr[i]
if (v[j][v[j].size() - 1] + 1 == arr[i]) {
if (pos == -1) {
pos = j;
size = v[j].size();
} else {
// Select the subsequence with minimum size
if (v[j].size() < size) {
size = v[j].size();
pos = j;
}
}
}
}
// If there is no subsequence that can accommodate the current element
// form a new subsequence
if (pos == -1) {
vector<int> newV;
newV.push_back(arr[i]);
v.push_back(newV);
} else {
v[pos].push_back(arr[i]);
}
}
for (int i = 0; i < v.size(); i++) {
if (v[i].size() < 3) {
return false;
}
}
return true;
}
int main() {
// Example 1
int arr1[] = {1, 2, 3, 3, 4, 5};
if(isPossible(arr1, sizeof(arr1) / sizeof(arr1[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 2
int arr2[] = {1, 2, 3, 3, 4, 4, 5, 5};
if (isPossible(arr2, sizeof(arr2) / sizeof(arr2[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 3
int arr3[] = {1, 2, 3, 4, 4, 5};
if (isPossible(arr3, sizeof(arr3) / sizeof(arr3[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}true true false
Complexity Analysis
Time Complexity = O(n2)
Space Complexity = O(n)
Optimal Approach for Split Array Into Consecutive Subsequences
For an element arr[i], either it can form a new subsequence or can be added to another subsequence ending at (arr[i] – 1), if there are more than one subsequence that can accommodate arr[i], add it to the subsequence of minimum length.
Only three types of subsequence length are important, that is, subsequences of length 1, length 2 and length greater than equals to 3, denoted as p1, c1, p2, c2, p3 and c3, where p means previous and c means current.
For every number first count the number of occurrences of it in the array, check if it can spread across all the subsequences of length 1 and 2, if it cannot, return false immediately, because if the current number cannot extend subsequences of length 1 or 2, no number will do as the array is sorted. So there will remain some subsequences of length 1 or 2 at the end.
Else all the subsequences of length 1 converts to subsequences of length 2, length 2 converts to length 3, and remaining elements are added to subsequences of length 3 or more, if still some elements are not distributed they contributes to subsequences of length 1, else only the elements contributing to length 3 or more adds to the new length 3 subsequences.
At the end, if there are no length 1 and length 2 subsequences return true, else return false.
JAVA Code
public class SplitArrayIntoConsecutiveSubsequences {
private static boolean isPossible(int[] arr) {
int n = arr.length;
if (n < 3) {
return false;
}
int p1 = 0, p2 = 0, p3 = 0;
int c1 = 0, c2 = 0, c3 = 0;
int i = 0;
// prev denotes previous element
// curr denotes current element
int prev = 0, curr = 0;
// Traverse the array
while (i < n) {
// Current becomes previous
p1 = c1;
p2 = c2;
p3 = c3;
prev = curr;
curr = arr[i];
int count = 0;
// Count the frequency of current element
while (i < n && arr[i] == curr) {
i++;
count++;
}
if (prev + 1 == curr) {
// if element cannot be spread across subsequences of length 1 and 2
if (count < p1 + p2) {
// return false immediately
return false;
}
// Update c1, c2, c3 as described
c1 = Math.max(0, count - (p1 + p2 + p3));
c2 = p1;
c3 = p2 + Math.min(p3, count - (p1 + p2));
} else {
// this element cannot be spread across any subsequence
if (p1 != 0 || p2 != 0) {
// if there is any subsequence of length 1 or 2
// return false immediately
return false;
}
// Update c1, c2, c3 as described
c1 = count;
c2 = 0;
c3 = 0;
}
}
// if there are no length 1 and length 2 subsequences return true, else return false
return (c1 == 0 && c2 == 0);
}
public static void main(String[] args) {
// Example 1
int arr1[] = new int[]{1, 2, 3, 3, 4, 5};
System.out.println(isPossible(arr1));
// Example 2
int arr2[] = new int[]{1, 2, 3, 3, 4, 4, 5, 5};
System.out.println(isPossible(arr2));
// Example 3
int arr3[] = new int[]{1, 2, 3, 4, 4, 5};
System.out.println(isPossible(arr3));
}
}true true false
C++ Code
#include<bits/stdc++.h>
using namespace std;
bool isPossible(int *arr, int n) {
if (n < 3) {
return false;
}
int p1 = 0, p2 = 0, p3 = 0;
int c1 = 0, c2 = 0, c3 = 0;
int i = 0;
// prev denotes previous element
// curr denotes current element
int prev = 0, curr = 0;
// Traverse the array
while (i < n) {
// Current becomes previous
p1 = c1;
p2 = c2;
p3 = c3;
prev = curr;
curr = arr[i];
int count = 0;
// Count the frequency of current element
while (i < n && arr[i] == curr) {
i++;
count++;
}
if (prev + 1 == curr) {
// if element cannot be spread across subsequences of length 1 and 2
if (count < p1 + p2) {
// return false immediately
return false;
}
// Update c1, c2, c3 as described
c1 = std::max(0, count - (p1 + p2 + p3));
c2 = p1;
c3 = p2 + std::min(p3, count - (p1 + p2));
} else {
// this element cannot be spread across any subsequence
if (p1 != 0 || p2 != 0) {
// if there is any subsequence of length 1 or 2
// return false immediately
return false;
}
// Update c1, c2, c3 as described
c1 = count;
c2 = 0;
c3 = 0;
}
}
// if there are no length 1 and length 2 subsequences return true, else return false
return (c1 == 0 && c2 == 0);
}
int main() {
// Example 1
int arr1[] = {1, 2, 3, 3, 4, 5};
if(isPossible(arr1, sizeof(arr1) / sizeof(arr1[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 2
int arr2[] = {1, 2, 3, 3, 4, 4, 5, 5};
if (isPossible(arr2, sizeof(arr2) / sizeof(arr2[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
// Example 3
int arr3[] = {1, 2, 3, 4, 4, 5};
if (isPossible(arr3, sizeof(arr3) / sizeof(arr3[0]))) {
cout<<"true"<<endl;
} else {
cout<<"false"<<endl;
}
return 0;
}true true false
Complexity Analysis
Time Complexity = O(n)
Space Complexity = O(1)