In evaluate division problem we have given some equations, in the form, A/B = k, where A and B are strings and k is a real number. Answer some queries, if the answer does not exist return -1.
Table of Contents
Example
Input:
equations: a/b = 2.0 and b/c = 3.0
queries: a/c = ?, b/a = ?, a/e = ?, a/a = ?, x/x = ?
Output:
{6.0, 0.5, -1.0, 1.0, -1.0}
Equations are represented as list of list of strings, values are represented as array of double and queries are also represented as list_of_list_of strings, that is, for above example, input is represented as
equations = {{“a”, “b”}, {“a”, “c”}}
values = {2.0, 3.0}
queries = {{“a”, “c”}, {“b”, “a”}, {“a”, “e”}, {“a”, “a”}, {“x”, “x”}}
Algorithm for Evaluate Division
The above problem represents a graph.
Variables in the equations are nodes and the value of equations is the weight of edges.
An edge from vertex x to vertex y has a weight equals to x / y.
The graph for the above example is,
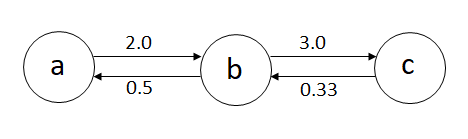
Answer to a query is found by doing a DFS search in the graph.
- Build the graph as mentioned above.
- Each query is of the form of source and destination, we have to start from the source and reach the destination.
- For every query, start from the source, if the source does not exists, return -1.
- If the source has a direct edge to the required destination, return the value of the edge.
- Else mark source as visited and recur for all the neighbors of source that are not visited yet, neighbor becomes the source and destination remains the same, if the answer of any of the neighbor is not -1, return edge weight from source to the neighbor plus answer of neighbor.
JAVA Code for Evaluate Division
import java.util.*;
public class EvaluateDivision {
private static double[] calcEquation(List<List<String>> equations, double[] values,
List<List<String>> queries) {
// Build the graph
HashMap<String, HashMap<String, Double>> graph = new HashMap<>();
for (int i = 0; i < equations.size(); i++) {
String from = equations.get(i).get(0);
String to = equations.get(i).get(1);
// From source to destination the weight of edge is values[i]
if (graph.containsKey(from)) {
graph.get(from).put(to, values[i]);
} else {
HashMap<String, Double> map = new HashMap<>();
map.put(to, values[i]);
graph.put(from, map);
}
// From destination to source the weight of edge is (1 / values[i])
if (graph.containsKey(to)) {
graph.get(to).put(from, 1 / values[i]);
} else {
HashMap<String, Double> map = new HashMap<>();
map.put(from, 1 / values[i]);
graph.put(to, map);
}
}
// Solve queries
double ans[] = new double[queries.size()];
for (int i = 0; i < queries.size(); i++) {
// Visited set
HashSet<String> visited = new HashSet<>();
ans[i] = dfs(graph, queries.get(i).get(0), queries.get(i).get(1), visited);
}
return ans;
}
private static double dfs(HashMap<String, HashMap<String, Double>> graph, String from, String to,
HashSet<String> visited) {
// Source not found
if (!graph.containsKey(from)) {
return -1.0;
}
// Direct edge
if (graph.get(from).containsKey(to)) {
return graph.get(from).get(to);
}
// Mark source as visited
visited.add(from);
for (Map.Entry<String, Double> entry : graph.get(from).entrySet()) {
if (!visited.contains(entry.getKey())) {
// For all unvisited neighbors of source do dfs
// neighbor becomes the source and destination remains same
double ans = dfs(graph, entry.getKey(), to, visited);
if (ans != -1.0) {
// If ans of any neighbor is not -1, return (edge weight * ans of neighbor)
return (ans * entry.getValue());
}
}
}
// All neighbors returned -1, return -1
return -1.0;
}
public static void main(String[] args) {
// Example
List<List<String>> equations = new ArrayList<>();
ArrayList<String> eq1 = new ArrayList<>();
eq1.add("a");
eq1.add("b");
equations.add(eq1);
ArrayList<String> eq2 = new ArrayList<>();
eq2.add("b");
eq2.add("c");
equations.add(eq2);
double values[] = new double[2];
values[0] = 2.0;
values[1] = 3.0;
List<List<String>> queries = new ArrayList<>();
ArrayList<String> q1 = new ArrayList<>();
q1.add("a");
q1.add("c");
queries.add(q1);
ArrayList<String> q2 = new ArrayList<>();
q2.add("b");
q2.add("a");
queries.add(q2);
ArrayList<String> q3 = new ArrayList<>();
q3.add("a");
q3.add("e");
queries.add(q3);
ArrayList<String> q4 = new ArrayList<>();
q4.add("a");
q4.add("a");
queries.add(q4);
ArrayList<String> q5 = new ArrayList<>();
q5.add("x");
q5.add("x");
queries.add(q5);
double ans[] = calcEquation(equations, values, queries);
for (int i = 0; i < ans.length; i++) {
System.out.print(ans[i] + " ");
}
}
}C++ Code for Evaluate Division
#include<bits/stdc++.h>
using namespace std;
double dfs(unordered_map<string, unordered_map<string, double>> &graph,
string from, string to, unordered_set<string> &visited) {
// Source not found
if (graph.find(from) == graph.end()) {
return -1.0;
}
// Direct edge
if (graph[from].find(to) != graph[from].end()) {
return graph[from][to];
}
// Mark source as visited
visited.insert(from);
for (auto i : graph[from]) {
if (visited.find(i.first) == visited.end()) {
// For all unvisited neighbors of source do dfs
double ans = dfs(graph, i.first, to, visited);
if (ans != -1.0) {
// If ans of any neighbor is not -1, return (edge weight * ans of neighbor)
return (ans * i.second);
}
}
}
// All neighbors returned -1, return -1
return -1.0;
}
vector<double> calcEquation(vector<vector<string>>& equations,
vector<double>& values,
vector<vector<string>>& queries) {
// Build the graph
unordered_map<string, unordered_map<string, double>> graph;
for (int i = 0; i < equations.size(); i++) {
string from = equations[i][0];
string to = equations[i][1];
// From source to destination the weight of edge is values[i]
if (graph.find(from) == graph.end()) {
unordered_map<std::string, double> m;
m.insert(make_pair(to, values[i]));
graph.insert(make_pair(from, m));
} else {
graph[from].insert(make_pair(to, values[i]));
}
// From destination to source the weight of edge is (1 / values[i])
if (graph.find(to) == graph.end()) {
unordered_map<std::string, double> m;
m.insert(make_pair(from, 1 / values[i]));
graph.insert(make_pair(to, m));
} else {
graph[to].insert(make_pair(from, 1 / values[i]));
}
}
// Solve queries
vector<double> ans;
for (int i = 0; i < queries.size(); i++) {
unordered_set<string> visited;
ans.push_back(dfs(graph, queries[i][0], queries[i][1], visited));
}
return ans;
}
int main() {
// Example
vector<vector<string>> equations;
vector<string> eq1;
eq1.push_back("a");
eq1.push_back("b");
equations.push_back(eq1);
vector<string> eq2;
eq2.push_back("b");
eq2.push_back("c");
equations.push_back(eq2);
vector<double> values;
values.push_back(2.0);
values.push_back(3.0);
vector<vector<string>> queries;
vector<string> q1;
q1.push_back("a");
q1.push_back("c");
queries.push_back(q1);
vector<string> q2;
q2.push_back("b");
q2.push_back("a");
queries.push_back(q2);
vector<string> q3;
q3.push_back("a");
q3.push_back("e");
queries.push_back(q3);
vector<string> q4;
q4.push_back("a");
q4.push_back("a");
queries.push_back(q4);
vector<string> q5;
q5.push_back("x");
q5.push_back("x");
queries.push_back(q5);
vector<double> ans = calcEquation(equations, values, queries);
for (int i = 0; i < ans.size(); i++) {
cout<<ans[i]<<" ";
}
return 0;
}6 0.5 -1 1 -1
Complexity Analysis
Time Complexity = O(q * (V + E)), where
q –> Number of queries
V –> Number of vertices in the graph(or number of variables)
E –> Number of edges in the graph(or number of equations)