We have a message that we want to deliver. We want the message to be of least size possible so that the costs incurred in sending the message is low. Here we use the Huffman Coding concept to reduce the size of the message.
Let’s assume that we have the following data
- Message:BCCABBDDABCCBBAEDDCC
- Each character is represented by it’s ASCII value(8 bits)
- The cost of the message=Cost of sending over one character X Length of the message
Table of Contents
Explanation for Huffman Coding
Thus, the size of the message=(8×20)=160 bits. The message above is sent over simply without any encoding making it expensive and we are
using an 8-bit representation when we’ve only got 5 distinct characters which can be represented with only 3 bits (8 combinations).
The below table shows each character and their representation when we use only 3 bits.
| A | 000 |
| B | 001 |
| C | 010 |
| D | 011 |
| E | 100 |
It looks like the cost incurred now shrinks to 20×3=60 bits but the encrypted message will be hard to decipher and thus has to be sent with the above table as well which will cost us another 15 bits making the total cost 115 bits.
The above method uses a fixed-size code for each character. This is where the Huffman method comes into the picture. Below is the summary of the process
- Arrange alphabets in increasing order of count
- Merge two small nodes to form a new node
Let us look into the process step by step:
Step1: Create a node for each alphabet and sort them by their frequency

Step2: Merge two nodes with the least frequency. The parent node’s value will be the sum of values from both the nodes
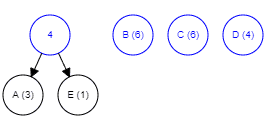
We keep repeating the second step until we obtain the binary tree.
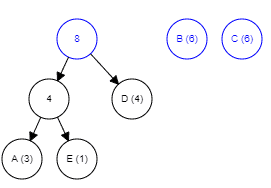

The tree obtained after merging all the nodes

Let us now obtain the encoding for all the alphabets
- Add a 0 to the representation every time you turn left
- Add a 1 to the representation every time you turn right
The below table lists the obtained codes
| A | 000 |
| B | 10 |
| C | 11 |
| D | 01 |
| E | 001 |
The size now reduces to 52 bits which is a considerable reduction in cost.
Now that we have understood the process let us look into the implementation for the same.
Java Program for Huffman Coding
import java.util.*;
//Node will represent all the letters with their frequency
class Node
{
int data;
char c;
Node left;
Node right;
}
class compare implements Comparator<Node>
{
public int compare(Node a,Node b)
{
return a.data-b.data;
}
}
public class huffman
{
public static void construct(Node root,String s)
{
//Identifying a root node
if(root.left==null && root.right==null && Character.isLetter(root.c))
{
System.out.println(root.c+":"+s);
return;
}
//Every time we turn left we add a zero to the code representation
construct(root.left,s+"0");
//Every time we turn right we add a one to the code representation
construct(root.right,s+"1");
}
public static void main(String args[])
{
int n=6;
char[] message= { 'a', 'b', 'c', 'd', 'e' };
int[] frequen= { 5, 5, 5, 4, 1 };
//Putting our data in min-priority queue
PriorityQueue<Node>q=new PriorityQueue<Node>(n,new compare());
for(int i=0;i<n;i++)
{
Node s=new Node();
s.c =message[i];
s.data=frequen[i];
s.left=null;
s.right=null;
q.add(s);
}
Node root=null;
//Extracting the sorted nodes from the queue
//Emptying until all we have is the root node
while(q.size()>1)
{
//Right for our root
Node rht=q.poll();
//Left for our root
Node lft=q.poll();
Node temp=new Node();
//Root will have the sum of data from both left and right
temp.data=rht.data+lft.data;
temp.c='-';
temp.left =lft;
temp.right=rht;
root=temp;
//Adding this to the queue to build up higher levels of the tree
q.add(temp);
}
construct(root,"");
}
}C++ Program for Huffman Coding
#include <iostream>
using namespace std;
#define MAX_TREE_HT 100
struct MinHeapNode
{
char data;
int freq;
struct MinHeapNode *left, *right;
};
struct MinHeap
{
unsigned size;
unsigned capacity;
struct MinHeapNode** array;
};
struct MinHeapNode* newNode(char data, unsigned freq)
{
struct MinHeapNode* temp = (struct MinHeapNode*)malloc(sizeof(struct MinHeapNode));
temp->left = temp->right = NULL;
temp->data = data;
temp->freq = freq;
return temp;
}
struct MinHeap* createMinHeap(unsigned capacity)
{
struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap));
minHeap->size = 0;
minHeap->capacity = capacity;
minHeap->array=(struct MinHeapNode**)malloc(minHeap-> capacity * sizeof(struct MinHeapNode*));
return minHeap;
}
void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b)
{
struct MinHeapNode* t = *a;
*a = *b;
*b = t;
}
void minHeapify(struct MinHeap* minHeap, int idx)
{
int smallest = idx;
int left = 2 * idx + 1;
int right = 2 * idx + 2;
if (left < minHeap->size && minHeap->array[left]-> freq<minHeap->array[smallest]->freq)
smallest = left;
if (right < minHeap->size && minHeap->array[right]->freq<minHeap->array[smallest]->freq)
smallest = right;
if (smallest != idx)
{
swapMinHeapNode(&minHeap->array[smallest],
&minHeap->array[idx]);
minHeapify(minHeap, smallest);
}
}
int isSizeOne(struct MinHeap* minHeap)
{
return (minHeap->size == 1);
}
struct MinHeapNode* extractMin(struct MinHeap* minHeap)
{
struct MinHeapNode* temp = minHeap->array[0];
minHeap->array[0] = minHeap->array[minHeap->size - 1];
--minHeap->size;
minHeapify(minHeap, 0);
return temp;
}
void insertMinHeap(struct MinHeap* minHeap, struct MinHeapNode* minHeapNode)
{
++minHeap->size;
int i = minHeap->size - 1;
while (i && minHeapNode->freq<minHeap->array[(i - 1) / 2]->freq)
{
minHeap->array[i] = minHeap->array[(i - 1) / 2];
i = (i - 1) / 2;
}
minHeap->array[i] = minHeapNode;
}
void buildMinHeap(struct MinHeap* minHeap)
{
int n = minHeap->size - 1;
int i;
for (i = (n - 1) / 2; i >= 0; --i)
minHeapify(minHeap, i);
}
void printArr(int arr[], int n)
{
int i;
for (i = 0; i < n; ++i)
cout<< arr[i];
cout<<"\n";
}
int isLeaf(struct MinHeapNode* root)
{
return !(root->left) && !(root->right);
}
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size)
{
struct MinHeap* minHeap = createMinHeap(size);
for (int i = 0; i < size; ++i)
minHeap->array[i] = newNode(data[i], freq[i]);
minHeap->size = size;
buildMinHeap(minHeap);
return minHeap;
}
struct MinHeapNode* buildHuffmanTree(char data[], int freq[], int size)
{
struct MinHeapNode *left, *right, *top;
struct MinHeap* minHeap = createAndBuildMinHeap(data, freq, size);
while (!isSizeOne(minHeap))
{
left = extractMin(minHeap);
right = extractMin(minHeap);
top = newNode('$', left->freq + right->freq);
top->left = left;
top->right = right;
insertMinHeap(minHeap, top);
}
return extractMin(minHeap);
}
void printCodes(struct MinHeapNode* root, int arr[], int top)
{
// Assign 0 to left edge and recur
if (root->left) {
arr[top] = 0;
printCodes(root->left, arr, top + 1);
}
// Assign 1 to right edge and recur
if (root->right) {
arr[top] = 1;
printCodes(root->right, arr, top + 1);
}
if (isLeaf(root)) {
cout<< root->data <<": ";
printArr(arr, top);
}
}
void HuffmanCodes(char data[], int freq[], int size)
{
// Construct Huffman Tree
struct MinHeapNode* root
= buildHuffmanTree(data, freq, size);
int arr[MAX_TREE_HT], top = 0;
printCodes(root, arr, top);
}
int main()
{
char arr[] = { 'a', 'b', 'c', 'd', 'e' };
int freq[] = { 5, 9, 12, 13, 16};
int size = sizeof(arr) / sizeof(arr[0]);
HuffmanCodes(arr, freq, size);
return 0;
}c: 00 d: 01 a: 100 b: 101 e: 11
Complexity Analysis
Let’s look into the time complexity:
The time that is taken for heapifying each node to the min-heap: log(n)
Number of nodes: n
Thus the time taken would be O(n log n)