Degree of an array

Difficulty Level Easy
Frequently asked in VMware Walmart Labs
Array Binary Search Hash SearchingViews 6078

Problem Statement

In the Degree of an array problem we have given a non-empty array of non-negative integers nums, the degree of this array is defined as the maximum frequency of any one of its elements.

Your task is to find the smallest possible length of a (contiguous) subarray of nums, that has the same degree as nums.

Input: [1, 2, 2, 3, 1]

Output: 2

Approach 1: Using binary search

arr: Given array

n: size of array

Let’s say the given array has degree k, now the minimum size of subarray which has the same degree can not be less than k and not be greater than n.

So if we run a binary search on the size of the subarray and check if it is possible to have a subarray of that size with degree k, then we can get the optimal answer.

Also, the search space of this binary search should be from k to n.

Algorithm

  1. Find the degree of the given array( let it be k).
  2. Take three variable left=k, right=n and ans=n.
  3. Run loop till left<=right:
    • Find the degree of (left+right)/2 size subarrays( let it be x).
    • If x==k, then ans=min(ans,x) and right = (left+right)/2 -1.
    • If x<k, then left = (left+right)/2 +1.
  4. Return ans.

Implementation

C++ Program for Degree of an array

#include<bits/stdc++.h>
using namespace std;
int findDegree(vector<int>& v, int k){
    unordered_map<int,int> m;
    int ans=0;
    for(int i=0;i<k;i++){
        m[v[i]]++;
        ans=max(ans,m[v[i]]);
    }
    for(int i=k;i<v.size();i++){
        m[v[i-k]]--;
        m[v[i]]++;
        ans=max(ans,m[v[i]]);
    }
    return ans;
}
int findShortestSubArray(vector<int>& nums) {
    int k=findDegree(nums,nums.size());
    int l=k,r=nums.size(),m,ans=nums.size();
    while(l<=r){
        m=l+(r-l)/2;
        int x=findDegree(nums,m);
        if(x==k){
            ans=m;
            r=m-1;
        }
        else{
            l=m+1;
        }
    }
    return ans;
}
int main(){
    int n;
    cin>>n;
    vector<int> arr(n);
    for(int i=0;i<n;i++){
        cin>>arr[i];
    }
    cout<<"The smallest possible length of a subarray of the given array, that has same degree is: "<<findShortestSubArray(arr);
}

7 
1 2 2 3 1 4 2

The smallest possible length of a subarray of the given array, that has same degree is: 6

Complexity

Time complexity: O(nlogn), we do logn search on size and in each search, we are traversing the array once.

Space complexity: O(1), no extra space required.

Approach 2: Using hashing

Let’s say we have the degree of the given array as k and the element which has maximum frequency is a, now we can conclude that the minimum size of subarray which has the same degree should start and end with a only.

Algorithm

  1. Take three hashmaps left, right and count.
  2. Run a loop on i from 0 to n:
    • If arr[i] is not in left, then insert {arr[i], i} in left.
    • Update {arr[i], i} in right.
    • Update {arr[i], count[arr[i]]+1} in count.
  3. Take a variable ans=n.
  4. For every arr[i] whose count[arr[i]]==k:
    • ans=min(right[arr[i]]-left[arr[i]]+1, ans)
  5. Return ans.

Example of Degree of an array

 

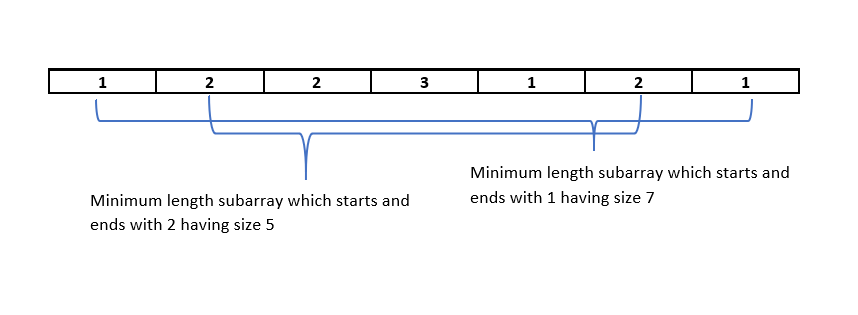
Degree of an array

Here we have two elements that has a maximum frequency of 3, these are 1 and 2.

Now we have two choices either we can take the subarray which starts and ends with 1 or 2.

We will choose the one which has a minimum length i.e., the answer will be 5.

Implementation

C++ program for the Degree of an array

#include<bits/stdc++.h>
using namespace std;
int findShortestSubArray(vector<int>& nums){
   unordered_map<int,int> left, right, count;
   int degree = 0;
    for (int i = 0; i < nums.size(); i++) {
        int x = nums[i];
        if (left.find(x)==left.end()) 
            left.insert({x,i});
        right[x]=i;
        count[x]++;
        degree=max(degree,count[x]);
    }
    int ans = nums.size();
    for (auto &it:count) {
        if (it.second == degree) {
            ans = min(ans, right[it.first] - left[it.first] + 1);
        }
    }
    return ans;
}
int main(){
    vector<int> arr={1, 2, 2, 3, 1, 4, 2};
    cout<<"The smallest possible length of a subarray of the given array, that has same degree is: "<<findShortestSubArray(arr);
}

The smallest possible length of a subarray of the given array, that has same degree is: 6

JAVA program for the Degree of an array

import java.util.*; 
public class Main
{
    public static int findShortestSubArray(int[] nums) {
        Map<Integer, Integer> left = new HashMap(),
            right = new HashMap(), count = new HashMap();

        for (int i = 0; i < nums.length; i++) {
            int x = nums[i];
            if (left.get(x) == null) left.put(x, i);
            right.put(x, i);
            count.put(x, count.getOrDefault(x, 0) + 1);
        }

        int ans = nums.length;
        int degree = Collections.max(count.values());
        for (int x: count.keySet()) {
            if (count.get(x) == degree) {
                ans = Math.min(ans, right.get(x) - left.get(x) + 1);
            }
        }
        return ans;
    }
  public static void main(String[] args) {
      int[] arr={1,2,3,4,4,3,2,2,4};
    System.out.println("The smallest possible length of a subarray of the given array, that has same degree is: "+findShortestSubArray(arr));
  }
}

The smallest possible length of a subarray of the given array, that has same degree is: 6

Complexity

Time complexity: O(n) as we are traversing the array and map at once.

Space complexity: O(n) as we used three hashmaps.

References

Translate »