Find a sorted subsequence of size 3 in linear time

Problem Statement

The problem “Find a sorted subsequence of size 3 in linear time” states that you have an integer array. The problem statement asks to find out the three numbers in such a way that array[i] < array [k] < array[k], and i < j < k.

Example

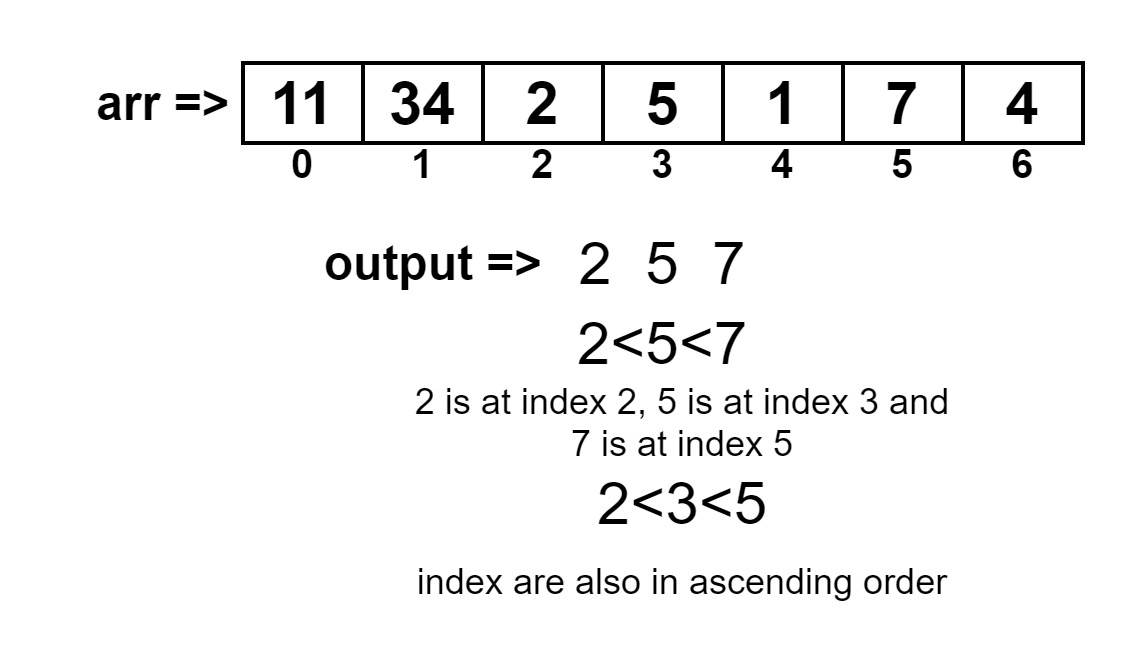
arr[] = {11,34,2,5,1,7,4 }

2 5 7

Explanation

2 is less than 5 and 5 is less than 7, and such that their indexes are less than each other.

Algorithm

1. Declare a new array “small” and “great” of size as same as the original array.
2. Set the value of maximum to n-1, and the value of minimum to 0.
3. Marked the first element of the array we created to -1.
4. Traverse the array from i=1 to less than n(n is the length of the array).
  1. Check if arr[i] is smaller or equal to arr[minimum], if true
    1. Set minimum to i and small[i] to -1.
  2. Else put small[i] = minimum.
5. Traverse the array from i=n-2 to less than equal to 0(n is the length of the array).
  1. Check if arr[i] is greater than or equal to arr[maximum], if true
    1. Set maximum to i and great[i] to -1.
  2. Else put great[i] = maximum.
6. Traverse the array from i=0 to n and check if small[i] and great[i] is not equal to -1, then print the arr[small[i]] , arr[i] and arr[great[i]].
  1. Return

Explanation

We have an array of integer. We have asked to find out the sorted subsequence in the given array. Sorted subsequence contains three numbers which we have to find in sorted order and it should be in sequence, not contiguously but in sequence, the first number should be less than the second number and second number should be less than the third number, and first, second and third should come in order.

We are going to traverse the array from 1 to less than n, we will leave the first and last index element as it is. Because we have marked those -1 in the two arrays we created, small and great. We marked their first and index element is equal to -1 of small and great arrays respectively. Traversing the array and check if arr[i] is less than or equal to arr[minimum] where minimum we marked as 0, if the condition is found to be true, then update the value of minimum to i, and marked current small array element to -1.

Same thing we will do with the great array, but with from the traversal of the array from the second element of the right side to 0. We will traverse the array and check if arr[i] is greater than or equal to arr[maximum], if it is true then we have to update the value of maximum to 0 and great[i] to -1. Else we will put the maximum as great[i]. After this, we will traverse the array again and check if small[i] and great[i] is not equal to -1, if it is true, then print the mentioned values.

Code

C++ code to Find a sorted subsequence of size 3 in linear time

#include<iostream>
using namespace std;

void getTriplet(int arr[], int n)
{
    int maximum = n - 1;
    int minimum = 0;
    int i;

    int* small = new int[n];

    small[0] = -1;
    for (i = 1; i < n; i++)
    {
        if (arr[i] <= arr[minimum])
        {
            minimum = i;
            small[i] = -1;
        }
        else
            small[i] = minimum;
    }

    int* great = new int[n];

    great[n - 1] = -1;
    for (i = n - 2; i >= 0; i--)
    {
        if (arr[i] >= arr[maximum])
        {
            maximum = i;
            great[i] = -1;
        }
        else
            great[i] = maximum;
    }

    for (i = 0; i < n; i++)
    {
        if (small[i] != -1 && great[i] != -1)
        {
            cout << arr[small[i]] << " " << arr[i] << " "<< arr[great[i]];
            return;
        }
    }

    cout << "3 numbers not found";

    delete[] small;
    delete[] great;

    return;
}
int main()
{
    int arr[] = { 11,34,2,5,1,7,4 };
    int n = sizeof(arr) / sizeof(arr[0]);
    getTriplet(arr, n);
    return 0;
}

2 5 7

Java Code to Find a sorted subsequence of size 3 in linear time

class SortedSubsequenceSize3
{
    public static void getTriplet(int arr[])
    {
        int n = arr.length;
        int maximum = n - 1;

        int minimum = 0;
        int i;

        int[] small = new int[n];

        small[0] = -1;
        for (i = 1; i < n; i++)
        {
            if (arr[i] <= arr[minimum])
            {
                minimum = i;
                small[i] = -1;
            }
            else
                small[i] = minimum;
        }
        int[] great = new int[n];

        great[n - 1] = -1;
        for (i = n - 2; i >= 0; i--)
        {
            if (arr[i] >= arr[maximum])
            {
                maximum = i;
                great[i] = -1;
            }
            else
                great[i] = maximum;
        }
        for (i = 0; i < n; i++)
        {
            if (small[i] != -1 && great[i] != -1)
            {
                System.out.println(arr[small[i]] + " " + arr[i] + " " + arr[great[i]]);
                return;
            }
        }
        System.out.println("3 numbers not found");
        return;
    }
    public static void main(String[] args)
    {
        int arr[] = { 11,34,2,5,1,7,4 };
        getTriplet(arr);
    }
}

2 5 7

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. We have traversed all the array elements. And because the size of the array is N. The time complexity is also linear.

Space Complexity

O(n) where “n” is the number of elements in the array. We have been storing the smaller and greater element for each array element. Thus the space complexity is also linear.