In find a triplet that sum to a given value problem we have given an array of integers (positive and negative numbers) and you have to find a triplet (3 elements) in array whose sum is equal to the given value X.
Table of Contents
Input Format
First-line containing two integer values N and X.
Second-line containing N integer values or input array.
Output Format
Print any triplet whose sum given to X. If there are more than one triplets found print any one of them. If no such triplet found print 0.
Constraints
- 1<=N<=100000
- -1e9<=a[i]<=1e9
- -1e9<=X<= 1e9
Examples
Input
6, 10
1, 5, 7, 3, 4, 2
Output
1 7 2
Input
8, 11
-1, 12, 5, 7, -2, -4, 5, 1
Output
-2 1 12
Input
8, 0
-1, 12, 5, 7, -2, -4, 5, 1
Output
-4 -1 5
Approach Using 3 Pointers for Find a Triplet That Sum to a Given Value
- Sort the given array first which will give us time complexity of (n log n)
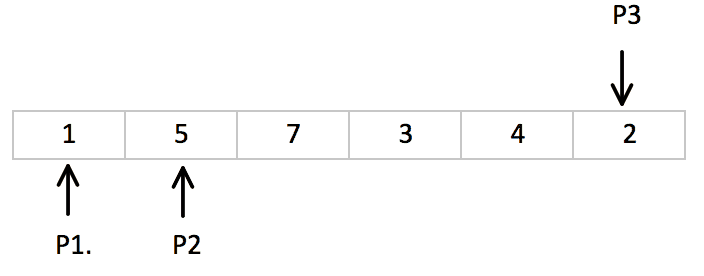
- Take 3 pointers p1, p2, p3 where p1 is pointing to start of the array, p2 will be pointing next to p1 and p3 will be pointing to the last index of an array.

- Have a loop1 to move (Increment) p1 till p1 < p3
- For each iteration of loop1 have loop2 to move (Increment) p2 till p2 < p3
- If sum of Array[p1] + Array[p2] + Array[p3] > k then Decrement p3
- If sum of Array[p1] + Array[p2] + Array[p3] == k then Print the elements
- p2 = p1 +1 and p3 = Array.length – 1
C++ Program for Find a Triplet That Sum to a Given Value
#include <bits/stdc++.h>
using namespace std;
void findTriplets(int arr[], int n, int k)
{
sort(arr,arr+n);
int p1=0, p2, p3, counter=0;
p2 = p1 + 1;
p3 = n-1;
while(p1<p3)
{
while(p2<p3)
{
if((arr[p1] + arr[p2] + arr[p3]) > k)
p3--;
if(((arr[p1] + arr[p2] + arr[p3]) == k)&&(p2<p3))
{
cout<<arr[p1]<<" "<<arr[p2]<<" "<<arr[p3]<<endl;
counter++;
goto label;
}
p2++;
}
p1++;
p2=p1+1;
p3=n-1;
}
if(counter==0)
cout<<0<<endl;
label:;
}
int main()
{
int n,x;
cin>>n>>x;
int a[n];
for(int i=0;i<n;i++)
{
cin>>a[i];
}
findTriplets(a,n,x);
return 0;
}6 10 1 5 7 3 4 2
1 2 7
Complexity Analysis for Find a Triplet That Sum to a Given Value
Time Complexity
O(n*n*n) where n is the length of the array. Here we use 3 pointer method to traverse in the array. In the worst case the loop will run N*N*N times.
Space Complexity
O(1) because here we don’t use any auxiliary space here.
Approach 2 for Find a Triplet That Sum to a Given Value
Here also we need to find the triplets from an array whose sum is equal to the given number.
Algorithm
1. First sort the input array
2. Fix the first element as arr[i], where i ranges from 0 to N-23. After fixing the first element, for finding the next two elements, take two pointer like variables ( j = i+1, k= N-1) and traverse the algorithm for finding the sum in sorted array.
4. while j is less than k Add the elements at the given indexes ie, arr[i] + arr[j] + arr[k] if Triplet sum is equal to the value X, print the three elements else if Triplet sum is less than the value X, then increase the j value else decrease the value of k.

C++ Program for Find a Triplet That Sum to a Given Value
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,x;
cin>>n>>x;
int a[n];
for(int i=0;i<n;i++)
{
cin>>a[i];
}
int flag=0;
sort(a,a+n);//sort the array in ascending order
int computed_sum;//sum computed at each step
//fix one element and search for other two elements in linear time
for(int i = 0; i <n-2; i++)
{
//jth index starts from the next element of selected and k always starts at the ending index
int j = i+1,k=n-1;
while(j<k)
{
//add the elements at the given indices
computed_sum=a[i]+a[j]+a[k];
if(computed_sum==x)
{
cout<<a[i]<<" "<<a[j]<<" "<<a[k];
return 1;
}
else if(computed_sum<x)
{
k--;
}
else
{
j++;
}
}
}
cout<<0<<endl;
return 0;
}8 0 -1 12 5 7 -2 -4 5 1
-4 -1 5
Complexity Analysis
Time Complexity
O(N2) where N is the size of the array. Here we fix I and then use two pointer methods for j and k values. This will take N*N time in the worst case.
Space Complexity
O(1) because we don’t use any auxiliary space.