In Finding K closest element problem we have given a sorted array and a value x. The problem is to find the K number of elements closest to x in the given array.
Given an array arr[] ={12, 16, 22, 30, 35, 39, 42,45, 48, 50, 53, 55, 56} and x = 35. Your task is to find the k=4 closest element to x.
Result: 30,39,42,45
Note that if x is in the array then it will be skipped in the output.
Table of Contents
Algorithm
- Declare and define a binary search method.
- Declare a function solution in which array[], x, and k are passed as an argument from the main function.
- Call a binary search function from solution function, which returns the position of x to cp in solution function.
- Set n to array length, left to cp-1, right to cp+1, and count to 0.
- Iterates in the while loop, over the array till the following condition, satisfies:
- left>=0 and
- right < n and
- count < k
- Open if block in while loop, in which conditions are given as:
- x – array[left]
- array[right] – x
- If satisfies the condition, then print array[left] and do left —.
- If above condition failed then print array[right] and do right++ and do count++ inside the loop.
- Open if block with conditions given as if (right = = n ), open the while loop with conditions given as count < k and left >= 0 if satisfies , then print array[left] and do count++.
- Again open second if block with conditions given as if (left < 0 ), open the while loop with conditions given as count < k and left >= 0, if satisfies, then print array[right] and do count++.
The approach behind is we will first do a binary search to find the point nearest index to x. Then, we will search left and right for K closest element.
Explanation for Finding K closest element
So we have our first task as we have to find the ‘k’ closest elements to x in the array which is sorted and all gonna make our task easier. For this, we can use a binary search method to find out the element position, with that our task becomes easier to find k closest elements.
So our main idea is to obtain the position of x and do some operations and find out the number with the least difference with x in the given array. For this, we are going to pass the arguments of arr[], x, and k. Arguments like arr, 0, length of the array, and the number of which we have to find the position are passed into a binary search function from which we obtain the value of the position. With this position we are going to set the value of left to just before the x and value of the right to just after the x, that is left = cp -1( just before the x) and right to cp+1 (just after the x).
Now if arr[left], means the number just before the x has a difference( x – arr[left] ) less than ( arr[right] –x ), means the number just after the x then print the value of arr[left] and do left–, for the next time, else print arr[right] and keep increasing the value od count by 1.
Example
Suppose array given:
arr={12, 16, 22, 30, 35, 39, 42, 45, 48, 50, 53, 55, 56};
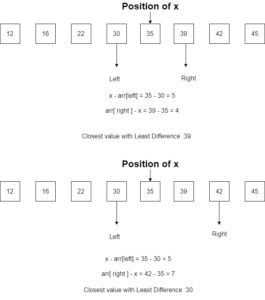
x=35, we got the position as 4 of 35.
Here left = cp -1 = 3 and right = cp + 1 = 5
Therefore, we compare x – arr[left] < arr[right] – x => 5 < 4, which fails the condition,
So in else block it will print arr[right] that is 39 and do right++ and count++ that is count=1.
Now left = 3 and right becomes 6
So we compare x – arr[left] < arr[right] – x => 5 < 7, which is true condition,
So in if block it will print arr[left] that is 30 and do left– and count++ that is count=2.
Now left=2 and right =6
So we compare x – arr[left] < arr[right] – x => 13 < 7, which is true condition,
So in else block it will print arr[right] that is 42 and do right++ and count++ that is count=3.
Now left=2 and right=7
So we compare x – arr[left] < arr[right] – x => 13 < 7, which fails the condition,
So in if else it will print arr[right] that is 42 and do right++ and count++ that is count=4.
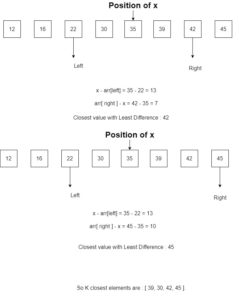
And now our count condition is failed means we got our all k closest elements.
And we have the answer as [39 30 42 45].
Implementation
C++ Program for Finding K closest element
#include<stdio.h>
int Binary_Search(int arr[], int low, int high, int x)
{
int mid = (low + high)/2;
if (arr[high] <= x)
return high;
if (arr[low] > x)
return low;
if (arr[mid] <= x && arr[mid+1] > x)
return mid;
if(arr[mid] < x)
return Binary_Search(arr, mid+1, high, x);
return Binary_Search(arr, low, mid - 1, x);
}
void solution(int arr[], int x, int k, int num)
{
int y = Binary_Search(arr, 0, num-1, x);
int r = y+1;
int count = 0;
if (arr[y] == x) y--;
while (y >= 0 && r < num && count < k)
{
if (x - arr[y] < arr[r] - x)
printf("%d ", arr[y--]);
else
printf("%d ", arr[r++]);
count++;
}
while (count < k && y >= 0)
printf("%d ", arr[y--]), count++;
while (count < k && r < num)
printf("%d ", arr[r++]), count++;
}
int main()
{
int arr[] = {12, 16, 22, 30, 35, 39, 42, 45, 48, 50, 53, 55, 56};
int num = sizeof(arr)/sizeof(arr[0]);
int x = 35;
int k = 4;
solution(arr, x, k, num);
return 0;
}39 30 42 45
Java Program for Finding K closest element
public class kce {
public static int binarySearch(int[] arr,int low, int high, int x){
int mid = 0;
while(low<=high){
mid = (high+low)/2;
if(arr[mid] == x){
return mid;
}
else if(x<arr[mid]){
high = mid-1;
}
else{
low = mid+1;
}
}
return mid;
}
public static void solution(int[] arr,int x, int k){
int cp = binarySearch(arr, 0, arr.length-1, x);
int n = arr.length-1;
int left = cp-1;
int right = cp+1;
int count = 0;
while(left>=0 && right<n && count <k){
if(x-arr[left]< arr[right] -x){
System.out.print(arr[left--] + " ");
left--;
}
else{
System.out.print(arr[right++] + " ");
right++;
}
count++;
}
if(right == n){
while(count<k && left>=0){
System.out.print(arr[left] + " ");
count++;
}
}
if(left < 0){
while(count<k && left>=0){
System.out.print(arr[right] + " ");
count++;
}
}
}
public static void main(String[]args){
int k = 4;
int x = 35;
int arr1[] = {12, 16, 22, 30, 35, 39, 42, 45, 48, 50, 53, 55, 56};
solution(arr1,x,k);
}
}
39 30 45 50
Complexity Analysis
Time Complexity
O(Logn+ K) where “n” is the size of the array and “k” is the number of the closest element we have to find.
Space Complexity
O(k) to store the required number of the closest elements.