Maximum length subsequence with difference between adjacent elements as either 0 or 1

Problem Statement

You are given an integer array. The problem “Maximum length subsequence with difference between adjacent elements as either 0 or 1” asks to find out the maximum subsequence length with the difference between the adjacent elements should be none other than 0 or 1.

Example

arr[] = {1, 4, 5, 2, 6, 5, 4, 8}

5

Explanation

Subsequence= 4, 5, 6, 5, 4

arr[] = {1, -3, -2, 0, -1, -2, -3, -4}

6

Explanation

Subsequence= -3, -2, -1, -2, -3, -4

Algorithm to find Maximum length subsequence with difference between adjacent elements as either 0 or 1

1. Declare a Map.
2. Set maxValue to 0.
3. Traverse the array starting from i=0 to while i<n (length of the array).
  1. Initialize a variable temp to 0.
  2. Check if Map contains the key as arr[i-1],
    1. If true, then get the value of arr[i-1] and store it to temp.
  3. Check if Map contains the key as arr[i],
    1. If true, then find the greater between the temp and the value of arr[i] in the map, and store it to temp.
  4. Check if Map contains the key as arr[i+1],
    1. If true, then find the greater between the temp and the value of arr[i+1] in the map, and store it to temp.
  5. Check if the temp is greater than maxValue,
    1. If true then store the value of temp to maxValue.
  6. And put the arr[i] as a key and temp as a value into the map.
4. Return maxValue.

Explanation

We are given an integer array, the problem statements ask to find out the maximum subsequence length . And the chosen subsequence should be such that it should have a difference between the adjacent values none other than 0 or 1. To solve this we will use hashing to make our solution efficient. We are going to put the key as array’s element and take the key’s value always find the maximum value and store it to temp.

Let us consider an example and understand this:

Example

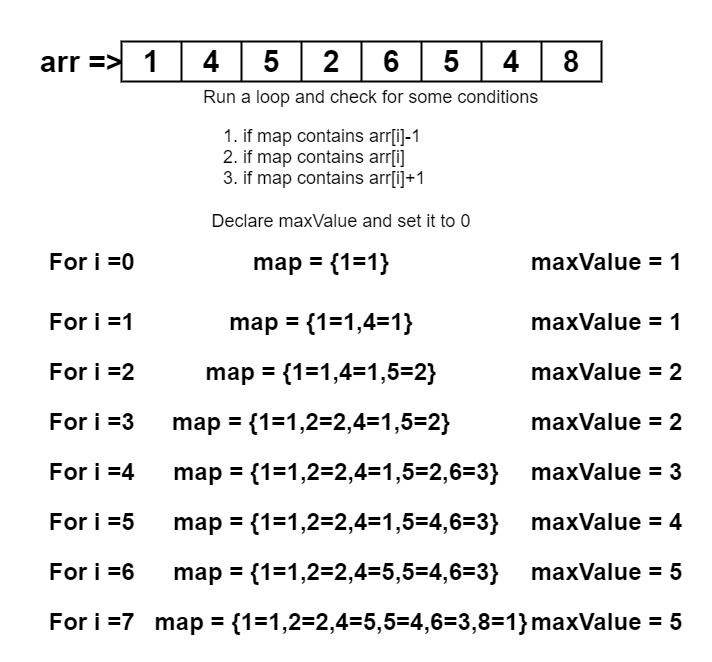
Arr[]={1, 4, 5, 2, 6, 5, 4, 8}

The first thing we do is to declare a map because we are going to store an array element and the value temp according to the algorithm we discussed. Set the value of maxValue to 0. We are going to return this variable. What is in that variable would be our answer. We will traverse the array and make it reach the length of the array. Every time we traverse the array with the new value of i, we initialize a value temp to 0.

i=0, arr[i] = 1, temp = 0, maxValue = 0  Map={}

Check which condition is going to fulfill. In this case, there is no condition. So it does temp++ and checks if the temp is greater than maxValue. If true then store the temp into maxValue and insert the value and temp into the map.

i=1, arr[i] = 4, temp = 0, maxValue = 1.

Map={1,1}

Same as above condition, we just insert the values into map

i=2, arr[i] = 5, temp = 0, maxValue = 1.

Map={1:1, 4:1}

This time we find the first condition correct that map contains the arr[i]-1 that is 4. So it takes the 1 as a temp and do temp++. Then change the maxValue to 2 and insert arr[i] and temp into it.

And simply like this, we are gonna keep checking the conditions and taking the values in temp. Keep on inserting it in a map, at last, we get the value in maxValue as our output.

Code

C++ code to find Maximum length subsequence with difference between adjacent elements as either 0 or 1

#include<iostream>
#include<unordered_map>

using namespace std;

int getMaximumLenSubsequence(int arr[], int n)
{
    unordered_map<int, int> MAP;
    int maxValue = 0;
    for (int i=0; i<n; i++)
    {
        int temp = 0;
        if (MAP.find(arr[i]-1) != MAP.end() && temp < MAP[arr[i]-1])
            temp = MAP[arr[i]-1];

        if (MAP.find(arr[i]) != MAP.end() && temp < MAP[arr[i]])
            temp = MAP[arr[i]];

        if (MAP.find(arr[i]+1) != MAP.end() && temp < MAP[arr[i]+1])
            temp = MAP[arr[i]+1];

        MAP[arr[i]] = temp + 1;

        if (maxValue < MAP[arr[i]])
            maxValue = MAP[arr[i]];
    }
    return maxValue;
}
int main()
{
    int arr[] = {1, 4, 5, 2, 6, 5, 4, 8};
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << getMaximumLenSubsequence(arr, n);
    return 0;
}

5

Java code to find Maximum length subsequence with difference between adjacent elements as either 0 or 1

import java.util.HashMap;

class subsequenceLength
{
    public static int getMaximumLenSubsequence(int[] arr)
    {
        int maxValue = 0;
        HashMap<Integer, Integer> MAP = new HashMap<>();
        for (int i = 0; i < arr.length; i++)
        {
            int temp = 0;
            if (MAP.containsKey(arr[i] - 1))
            {
                temp = MAP.get(arr[i] - 1);
            }

            if (MAP.containsKey(arr[i]))
            {
                temp = Math.max(temp, MAP.get(arr[i]));
            }

            if (MAP.containsKey(arr[i] + 1))
            {
                temp = Math.max(temp, MAP.get(arr[i] + 1));
            }
            temp++;
            if (temp > maxValue)
            {
                maxValue = temp;
            }
            MAP.put(arr[i], temp);
        }
        return maxValue;
    }
    public static void main(String[] args)
    {
        int arr[] = { 1, 4, 5, 2, 6, 5, 4, 8};
        System.out.println(getMaximumLenSubsequence(arr));
    }
}

5

Complexity Analysis

Time Complexity

O(n) where “n” is the number of elements in the array. We have simply traversed over all the elements in array. Because we have used HashMap we were able to do it in Linear time complexity.

Space Complexity

O(n) where “n” is the number of elements in the array. Since we are storing data related to elements in the map, the space complexity is also linear.