Maximum Product Subarray

Difficulty Level Medium
Frequently asked in Amazon Apple Bloomberg Facebook Google Microsoft
Array Dynamic ProgrammingViews 2391

In the maximum product subarray problem, we have given an array of integers, find the contiguous sub-array with atleast one element which has the largest product.

Example

Arr=[ 0, -1, 0 ,1 ,2, -3]

Maximum product = 2

Arr=[-1, -1, -1]

Maximum product = -1

Arr=[0, -1, 0, -2, 0]

Maximum product = 0

For Array Contains Only Positive Values

Let’s solve this problem first when the array contains only non-negative integers.

In that case we can have a positive product if a sub-array does not contain a zero. Hence the answer will the maximum of products of subarrays without a zero.

Lets take an example:

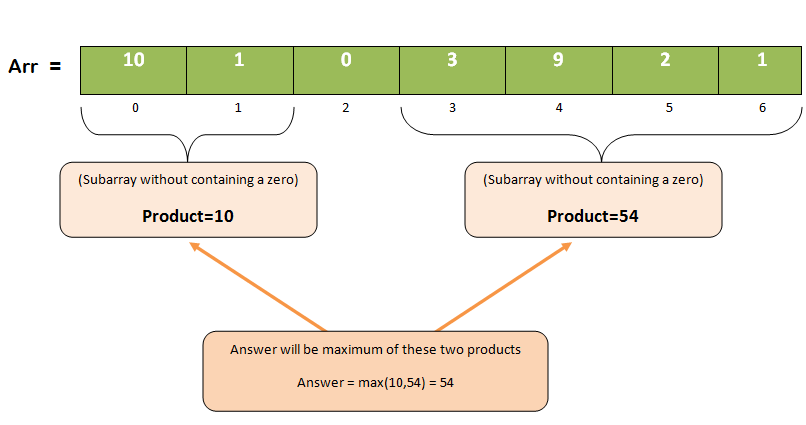
Maximum Product Subarray

C++ Program for Maximum Product Subarray

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n=7;
    int arr[]={10, 1, 0, 3, 9, 2, 1};
    int ans=0,curr_product=0;
    for(int i=0;i<n;i++){
        if(arr[i]==0){
            ans=max(ans,curr_product);
            curr_product=0;
        }
        else{
            curr_product=max(arr[i]*curr_product,arr[i]);
        }
    }
    ans=max(ans,curr_product);
    cout<<ans;
}

54

For Array Also Contains Negative Values

Now, what if the array also contains negative values?

In that case, we can’t ensure that the maximum product ending with  (i-1)th index will multiply with arr[i] to give an optimal answer.

For example:

arr = [1 -2 -3]

Maximum product till:

  • if i = 0 is 1
  • i = 1 is 1
  • i = 2 is 6 (-2*-3)

To overcome this issue, we can simply create two arrays:

  1. One to store maximum product ending at ith index.
  2. Other to store minimum product ending at ith index.

Now you have three options at every position in the array:

  1. Multiply the current element with maximum product calculated so far.
  2. Multiply the current element with minimum product calculated so far.
  3. Take current element as the starting position for maximum product sub
    array.

C++ Program for Maximum Product Subarray

#include<bits/stdc++.h>
using namespace std;
int maxProduct(int n,int a[]) {
    int mini[n];       // minimum product ending with ith index
    int maxi[n];       // maximum product ending with ith index
    
    mini[0]=a[0];
    maxi[0]=a[0];
    
    int ans = a[0];
    for(int i=1;i<n;i++) 
    {
        if(a[i]>0)
        {
            maxi[i] = max(maxi[i-1]*a[i], a[i]);
            mini[i] = min(mini[i-1]*a[i], a[i]);
        }
        else
        {
            maxi[i] = max(mini[i-1]*a[i], a[i]);
            mini[i] = min(maxi[i-1]*a[i], a[i]);
        }
        ans = max(ans, maxi[i]);
    }

    return ans;
}
int main(){
    int n;
    cin>>n;
    int a[n];
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int ans =maxProduct(n,a);
    cout<<"Maximum product of a subarray in the given array is "<<ans;
}

5
-2 7 5 -2 1

Maximum product of a subarray in the given array is 140

JAVA Program

import java.util.Scanner;

class Main{ 
static int maxProduct(int a[], int n) 
{ 
  int mini[] = new int[n];       // minimum product ending with ith index
    int maxi[] = new int[n];       // maximum product ending with ith index
    
    mini[0]=a[0];
    maxi[0]=a[0];
    
    int ans = a[0];
    for(int i=1;i<n;i++) 
    {
        if(a[i]>0)
        {
            maxi[i] = Math.max(maxi[i-1]*a[i], a[i]);
            mini[i] = Math.min(mini[i-1]*a[i], a[i]);
        }
        else
        {
            maxi[i] = Math.max(mini[i-1]*a[i], a[i]);
            mini[i] = Math.min(maxi[i-1]*a[i], a[i]);
        }
        ans = Math.max(ans, maxi[i]);
    }

    return ans;
} 

  public static void main(String[] args) { 
  Scanner sc = new Scanner(System.in);
    int n;
    n = sc.nextInt();	
  int a[] = new int[n]; 
  for(int i=0;i<n;i++){
      a[i] = sc.nextInt();
  }
    System.out.println("Maximum product of a subarray in the given array is "+maxProduct(a, n)); 
  } 
}

6
4 6 -2 -9 -3 1

Maximum product of a subarray in the given array is 432

Complexity Analysis for Maximum Product Subarray

Time Complexity: O(n) where n is the length of an array, as only one traversal of the array is required.

Space Complexity: O(n) because we use two arrays for storing the minimum and maximum products for each position.

References

Translate »