Ankur and Rishabh are two friends and want to buy some fruits from the market. They both have a list of their favourite fruit represented by strings. Your task is to help them find out their common favourite fruit with the minimum index sum. If there is a tie in the choice between them then output all of them with no order requirement. You can assume that there will always exist an answer.
Table of Contents
Example
Input
[“Apple”, “Orange”, “Mango”, “Lichi”]
[“Guava”, “Strawberry”, “Lichi”]
Output
Lichi
Explanation
Lichi is the only common fruit between them.
Input
[“Orange”, “Mango”, “Lichi”, “Apple”, “Strawberry”]
[“Strawberry”, “Orange”, “Apple”]
Ouput
Orange
Explanation
The fruit which is favourite of both and has the least index sum is “Orange” with index sum 1 (0+1).
Algorithm for Minimum Index Sum of Two Lists
- Get the two lists as our input values.
- Declare the map and a Vector.
- Add the values of list1 into the map with their indexes.
- Traverse the list2 and check if the element of list2 is present in the map and set ‘minimum’ to the maximum value of the integer.
- If found then store the sum of the current index and found element index into sum and store into sum.
- Check if the minimum is less than the sum if true then store sum into a minimum.
- Clear the resultant vector and store the new element.
- If the sum is equal to the minimum then simply add the value into the resultant vector.
- Print the output vector, we will get our answer.
Explanation
First of all, we are two lists as commonThings1 and commonThings2. These are our input values. So what we are going to do is we are going to pass these lists into our function in which we going to find our output.
We get those lists in which some strings are store in it as list1 and list2 as our input. We are going to use hashing and using a HashMap as our collection. Using HashMap we can store the elements into Map and their indexes, indexes help us to find out the least index sum. We can declare a vector of string “output” in which we going to store our output and later print that.
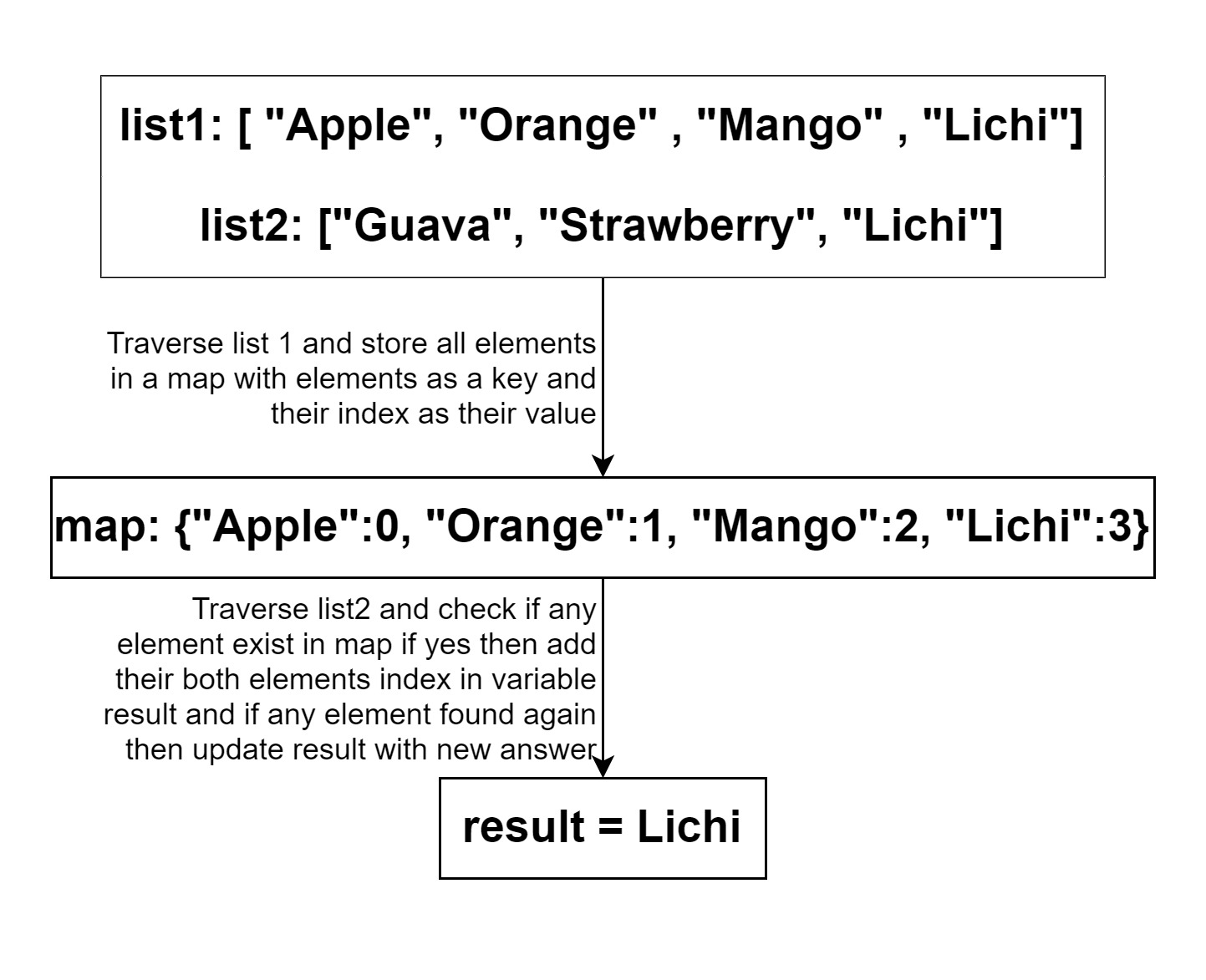
So we can take an example to understand this.
list1: [ “Apple”, ”Orange” , ”Mango” , “Lichi”]
list2: [“Guava”, “Strawberry”, “Lichi”]
We will traverse the list1 and add all the value of list1 into the map. Then we will check for the list2 elements if the map contains any one of the list element then we found the item, but we will search for the least minimum index, for that we will be declaring the sum and minimum, we will be checking the list1 element index and list2 element index we found, the sum of them is minimum of all, if we found minimum then we clear the resultant output and make a new entry in that, and also if two elements least index sum is equal, previous and current, then we will just push the new element.
In the example, we have taken, in this. we have only match found that is Lichi, and of the least minimum index and in all of that it is the only element found in the lists.
C++ Program for Minimum Index Sum of Two Lists
#include<bits/stdc++.h>
#include<unordered_map>
#include<vector>
using namespace std;
void getCommonString(vector<string> list1, vector<string> list2)
{
unordered_map<string, int> map;
for (int index = 0; index < list1.size(); index++)
map[list1[index]] = index;
vector<string> output;
int minimum = INT_MAX;
for (int j = 0; j < list2.size(); j++)
{
if (map.count(list2[j]))
{
int sum = j + map[list2[j]];
if (sum < minimum)
{
minimum = sum;
output.clear();
output.push_back(list2[j]);
}
else if (sum == minimum)
output.push_back(list2[j]);
}
}
for (int i = 0; i < output.size(); i++)
cout << output[i] << " ";
}
int main()
{
vector<string> commonThings1;
commonThings1.push_back("Apple");
commonThings1.push_back("Orange");
commonThings1.push_back("Mango");
commonThings1.push_back("lichi");
vector<string> commonThings2;
commonThings2.push_back("Guava");
commonThings2.push_back("Strawberry");
commonThings2.push_back("lichi");
getCommonString(commonThings1, commonThings2);
return 0;
}
lichi
Java Program for Minimum Index Sum of Two Lists
import java.util.HashMap;
import java.util.Vector;
class commonThings
{
public static void getCommonString(Vector<String> list1, Vector<String> list2)
{
Vector<String> output = new Vector<String>();
HashMap<String, Integer> map = new HashMap<>();
for (int index = 0; index < list1.size(); index++)
map.put(list1.get(index), index);
int minimum = Integer.MAX_VALUE;
for (int j = 0; j < list2.size(); j++)
{
if (map.containsKey(list2.get(j)))
{
int sum = j + map.get(list2.get(j));
if (sum < minimum)
{
minimum = sum;
output.clear();
output.add(list2.get(j));
}
else if (sum == minimum)
output.add(list2.get(j));
}
}
for (int i = 0; i < output.size(); i++)
System.out.println(output.get(i) + " ");
}
public static void main(String[] args)
{
Vector<String> commonThings1 = new Vector<String>();
commonThings1.add("apple");
commonThings1.add("mango");
commonThings1.add("banana");
commonThings1.add("lichi");
Vector<String> commonThings2 = new Vector<String>();
commonThings2.add("guava");
commonThings2.add("strawberry");
commonThings2.add("lichi");
getCommonString(commonThings1, commonThings2);
}
}
lichi
Complexity Analysis for Minimum Index Sum of Two Lists
Time Complexity
O(l1+l2), where l1 and l2 are the lengths of list1 and list2.
Space Complexity
O(l*x) where x is the length of the resultant list used to store the result and l is the maximum string length.