Partition Equal Subset Sum

Difficulty Level Medium
Frequently asked in Amazon Facebook Google
Array Dynamic ProgrammingViews 2561

Partition Equal Subset Sum is a problem in which we have given an array of positive numbers. We have to find out that can we divide it into two subsets such that the sum of elements in both sets is the same. Here it’s not necessary that the number of elements present in the set is equal. We can pick elements randomly from anywhere but every element picks just only one time. Here if the sum of elements presents in the array odd then we can’t divide it into two subsets. Let’s see how to pick elements from the array such that the sum of elements in both sets are remain the same.

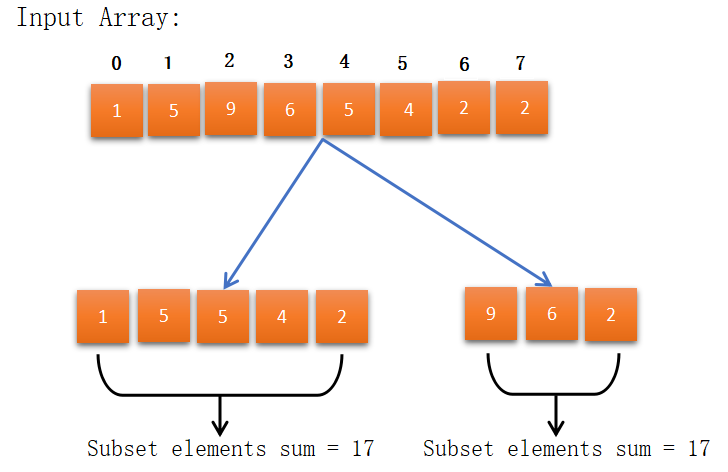
Partition Equal Subset Sum

Here we got sum of elements in both the subsets equal to 17. So we print “YES”.

Input Format

First-line containing an integer value N which tells the elements present in the array.

Second-line containing N integers.

Output Format

Only one line containing “YES” if we divide elements into two subsets otherwise print “NO”.

Constraints

  • 1<=N<=500
  • 1<=A[i]<=100
Sample Input:
8
1 5 9 6 5 4 2 2
Sample Output:
YES

Working Procedure

We just check whether we find any subset of the sum equal to half of the overall sum of the input array. So, we find this using Dynamic Programming approach. We create a DP matrix which contain 0 and 1. If there is one in any cell then we say we can create a set whose sum equal to the column value in which the value is true. Let’s see how we create this DP by the above example.

Step-1

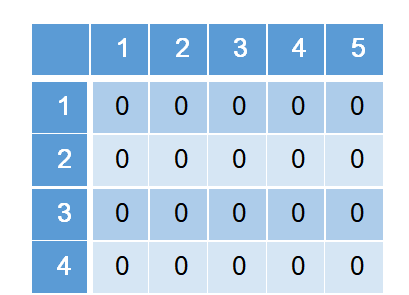
Lets take an example we have given array = {1, 2, 5, 2}, then TOTAL SUM=10 and subset sum = SUM = 10/2 =5.

Create a dp matrix of size N*SUM containing 0 in all cells initially.

Partition Equal Subset Sum

 

Step-2

Assign 1 in the first row and those columns in which we find the sum using 1st element of the input array.  Here we find sum = 1 using only 1st element of the array. So, our DP matrix looks like:

Step-3

Assign 1 in the second row and those columns in which we find the sum using starting 2 elements of the input array.  Here we find sum = {1, 2, 3} using only the first 2 elements of the array. So, our DP matrix looks like:

Step-4

Assign 1 in the third row and those columns in which we find the sum using starting 3 elements of the input array.  Here we find sum = {1, 2, 3, 5} using only the first 3 elements of the array. So, our DP matrix looks like:

Step-5

Assign 1 in the fourth row and those columns in which we find the sum using starting 3 elements of the input array.  Here we find sum = {1, 2, 3, 4, 5} using only the first four elements of the array. This is our last step because we visit all the rows. So, our DP matrix looks like:

Here we see that we can form a subset whose sum of elements is 5 because our DP array contain in the 4th row and 5th column as 1.

In this case, our code output is “YES”.

Algorithm

Step:1 Find the sum of all the elements of the given array.
Step:2 Set SUM = total sum of elements)/2.
Step:3 Create a DP matrix of size N*(SUM+1) where N is the number of elements in the input array.
Step:4 Set all the cells of DP matrix as 0.
Step:5 For i in range 0 to N:
       Set DP[i][0] = 1
Step:6 For i in range 1 to N:
           For j in range 1 to SUM:
                If arr[i-1] <= j then:
                   DP[i][j] = (DP[i-1][j]||DP[i-1][j-arr[i-1]])
                Else:
                   DP[i][j] = DP[i-1][j].
Step:7 If DP[N][SUM] is 1 then print "YES" else print "NO".

Implementation

/*C++ Implementation of Partition equal subset sum.*/ 
#include<bits/stdc++.h> 
using namespace std; 
bool partition(vector<int>nums,int sum)
{
    int n=nums.size();
    /**/
    int dp[n+1][sum+1];
    memset(dp,0,sizeof(dp));
    /*Set all cells of first column as 1.*/
    for(int i=0;i<=n;i++)
    {
        dp[i][0]=1;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=sum;j++)
        {
            /*update answer for each row.*/
            if(nums[i-1]<=j)
            {
                dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i-1]];
            }
            else dp[i][j]=dp[i-1][j];
        }
    }
    /*return the result.*/
    return dp[n][sum];
}
bool canPartition(vector<int>& nums) 
{
    int sum=0;
    for(int i=0;i<nums.size();i++)
    {
        sum+=nums[i];
    }
    if(sum%2!=0)
    {
        return 0;
    }
    return partition(nums,sum/2);   
}
int main() 
{ 
    /*input values.*/ 
    int n;  
    cin>>n;  
    vector<int> inp; 
    for(int i=0;i<n;i++) 
    { 
       int x; 
       cin>>x; 
       inp.push_back(x); 
    }  
    /*call the function.*/
    bool flag=canPartition(inp);
    /*print the answer.*/
    if(flag)
    {
        cout<<"YES"<<endl;
    }
    else
    {
        cout<<"NO"<<endl;
    }
    return 0; 
}
4
1 2 5 2
YES

Time Complexity

O(N*SUM) where N is the number of elements in the array and SUM is half of the total sum of the elements in the array. We traverse all the DP matrix of size N*SUM that’s why our time complexity is O(N*SUM).

Space Complexity

O(N*SUM) where N is the number of elements in the array and SUM is half of the total sum of the elements in the array. We create a DP matrix that tells us whether it’s possible to form the SUM using elements or not. In DP matrix DP[N][SUM] give the detail about the final answer so we need to store all the values in DP matrix.

References

Translate »