Peak Index in a Mountain Array

Difficulty Level Easy
Frequently asked in Microsoft
Array Binary SearchViews 6304

What is Peak Index in a Mountain Array Problem?

An array can be said as a Mountain Array if it shows the following properties:

  1. The length of the given array is should be greater than or equal to 3 LENGTH >=3.
  2. There can be only one peak or largest element in the array.
  3. It should follow : ARRAY[0] < ARRAY[1] < ARRAY[i-1] < ARRAY[ i] > ARRAY[ i+1 ] > ARRAY[..] > ARRAY[length-1]

Our task is to find the peak index in mountain array.

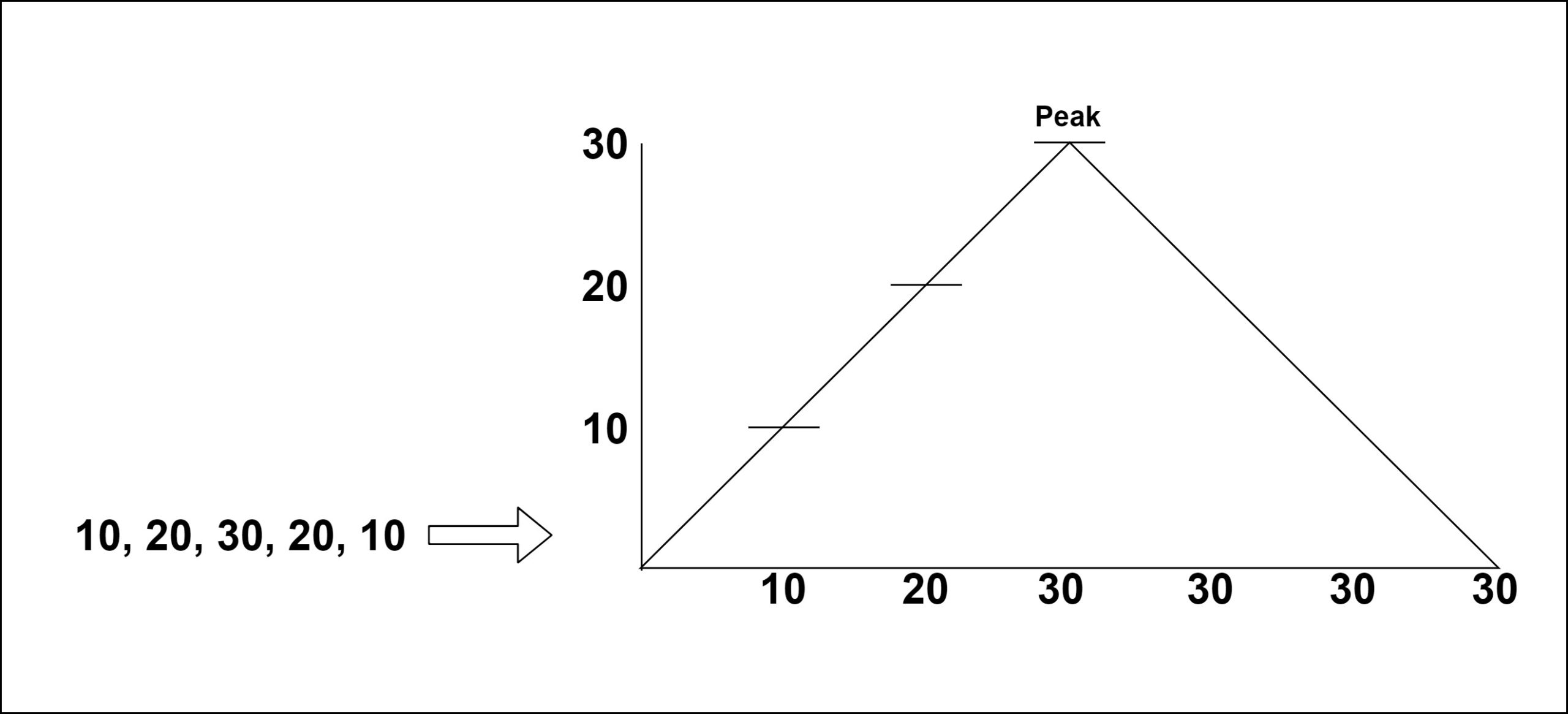
Example

Input

[10, 20, 30, 20, 10]

Output

2

Explanation

Index “2” i.e., “30” has the largest value.

Peak Index in a Mountain Array

Input

[0, 2, 1, 0]

Output

1

Explanation

Index “1” i.e., “2” has the largest value.

Algorithm

  1. Set low to 0.
  2. Set high to the length of array minus 1.
  3. Declare a variable mid.
  4. Set mid = low + ( high – low ) / 2.
  5. While low < high:
    1. If array[ mid ] > = array [ mid + 1].
      1. then high = mid.
    2. Else
      1. then low = mid + 1.
  6. Return low.

Explanation

So we have to find the peak index in a given array. For this we gonna use a binary search approach a little. We have function declare in our code named as getPeakIndex in which we pass our input array and the length of an array.

We declared a mid and initialize to 0 and high is equal to high-1, we are going to open a while loop and it will last until it false the condition of low < high. Entering in a loop we set mid=low+(high-low) / 2.

Example

Our input values are:{4,8,16,32,27,9,3};

So the value of high will be array length -1 => 7 – 1 = 6

High=6

Low=0

mid=low+(high-low) / 2 => 0 + ( 6 – 0) / 2 = 3

mid = 3.

Now it gonna checwok if ( array [ mid ] >= array[ mid+1 ] )

i.e, 32 is greater than or equal to 27 the condition is going to be true and set high = mid

So now low=0,

High=3,

Mid=3;

mid=low+(high-low) / 2 => 0 + ( 3 – 0) / 2 = 1

mid = 1.

Now it gonna check if ( array [ mid ] >= array[ mid+1 ] )

i.e, 8 is greater than or equal to 16 the condition is going to be false and execute else part and set low = mid +1;

So now low=2,

High=3,

Mid=1;

mid=low+(high-low) / 2 => 2 + ( 3 – 2) / 2 = 2

mid = 2.

Now it gonna check if ( array [ mid ] >= array[ mid+1 ] )

i.e, 16 is greater than or equal to 32 the condition is going to be false and execute else part and set low = mid +1;

So now low=3,

High=3,

Mid=3;

And here when it comes in loop while ( low < high ), means 3< 3 and it is false

And comes out of loop and return low i.e, low=3.

And the output will become :

peak index is : 3

Implementation in C++

#include <iostream>
using namespace std;

int peakIndex(int arr[],int high)
{
    int low=0;
    int mid;
    high-=1;
    while( low < high )
    {
        mid = low +(high - low)/2;
        if(arr[mid]>=arr[mid+1])
        {
            high=mid;
        }
        else
        {
            low=mid+1;
        }
    }
    return low;
}
int main()
{
    int mountainArray[]= {4,8,16,32,27,9,3};
    int n = sizeof(mountainArray)/sizeof(mountainArray[0]);
    int peak=peakIndex(mountainArray,n);
    cout<<"Peak index is:"<<peak;
    return 0;
}
Peak index is:3

Implementation in Java

class peakIndex {
  public static int getPeakIndex(int[] array) {
    int low = 0;
    int high = array.length - 1;
    int mid;
    while (low<high) {
      mid = low + (high - low) / 2;
      if (array[mid] >= array[mid + 1]) {
        high = mid;
      } else {
        low = mid + 1;
      }
    }
    return low;
  }

  public static void main(String[] args) {
    peakIndex pi = new peakIndex();
    int mountainArray[] = { 4, 8, 16, 32, 27, 9, 3 };
    int peak = getPeakIndex(mountainArray);
    System.out.println("Peak index is:" + peak);
  }
}
Peak index is:3

Complexity Analysis

Time Complexity

O(log n) where n is the length of the array.

Space Complexity

O(1) because we don’t use any extra or auxiliary space for evaluation.

References

Translate »