Queries for Decimal Values of Subarrays of a Binary Array

Difficulty Level Medium
Frequently asked in Amazon Google
Array Query ProblemViews 1215

Write Queries for decimal values of subarrays of a binary array in a given binary array. The problem statement asks to find out the decimal number so formed with the help of range in a binary array.

Example

Input:

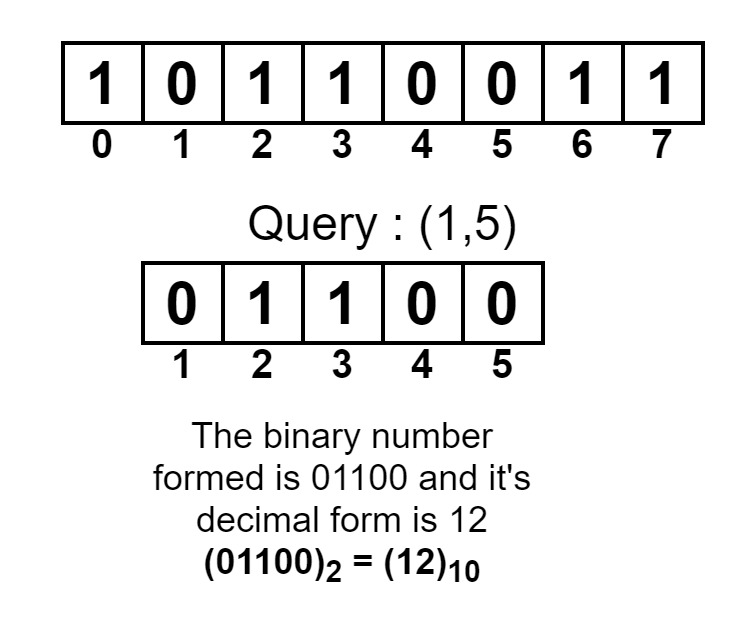
arr[] = {1, 0, 1, 1, 0, 0, 1, 1}

Query(1, 5)

Query(3, 6)

Output:

12 9

Explanation:

The output so formed as the binary numbers representing within a range of 1 to 5 inclusive (01100), is 12.

The output so formed as the binary numbers representing within a range of 3 to 6 inclusive (1001), is 9.

Queries for decimal values of subarrays of a binary array

 

Algorithm for Queries for decimal values of subarrays of a binary array

  1. Create an array as prefixArray, initialize it with the 0.
  2. Copy the last element of the prefixArray to the last element of the array given.
  3. Traverse through the array from right to left of the array, and store the product of the given array element and the powers of 2, and add it with the prefixArray.
  4. Get the query, if the value right is not equal to the last index value of the given array, return the division of the difference of the prefixArray[left] and prefixArray[right+1] and the shift operation of the 1 and the right index of the array.
  5. Else return the division of the prefixArray[left] and the shift operation of the 1 and the right index of the array.

Explanation for Queries for decimal values of subarrays of a binary array

Regarding the problem Queries for decimal values of subarrays of a binary array, Given a binary array and a range of indexes as a left index and right index. Find the decimal form of the given binary number so formed with the given range. We will be given a query in which we have given a range. We have to find the decimal number so formed of the binary number with the range. For this, we are going to create an extra array of the size the same as the length of the array. We will be building that array or we can say we can pre preprocess that array and fill some values in it so that we can solve the query in constant time.

Traverse through the array, but before traversing the array, fill the array with 0. In java when the array is created it is automatically filled with the 0, but in C++ we have to do it on our own. After that, get the product of the last array element and 1, save the value in the last element of the prefixArray. Now start from the right to left, means starting from the 2nd the last element of the array, now get the product of the numbers in powers of 2 and the given array element and add it with the previous value of prefixArray. Keep adding it with the values of the prefixArray and store it to the respective place of the prefixArray.

For each query given to us, check if the right value given is not equal to the last index of the array. If it is found to be true, then get the difference prefixArray[left] and prefixArray[right] and divide it with the value so formed when we apply the shift operation in the powers of 2 and return that value, else simply return the difference of prefixArray[left] and divide it with shift operation on the right value and return it.

Implementation

C++ program

#include<iostream>
#include<stdio.h>
#include<math.h>
#include<string.h>

using namespace std;

void buildArray(int arr[], int n, int prefixArray[])
{
    memset(prefixArray, 0, n * sizeof(int));
    prefixArray[n - 1] = arr[n - 1] * pow(2, 0);
    for (int i = n - 2; i >= 0; i--)
        prefixArray[i] = prefixArray[i + 1] + arr[i] * (1 << (n - 1 - i));
}
int getDeimalNum(int arr[], int left, int right, int n, int prefixArray[])
{
    if (right!= n - 1)
        return (prefixArray[left] - prefixArray[right + 1]) / (1 << (n - 1 - right));

    return prefixArray[left] / (1 << (n - 1 - right));
}
int main()
{
    int arr[] = {1, 0, 1, 1, 0, 0, 1, 1 };
    int n = sizeof(arr) / sizeof(arr[0]);

    int prefixArray[n];
    buildArray(arr, n, prefixArray);
    cout << getDeimalNum(arr, 1, 5, n, prefixArray) << endl;
    cout << getDeimalNum(arr, 3, 6, n, prefixArray) << endl;
    return 0;
}

12
9

Java program

import java.util.Arrays;

class DecimalfromSubArray
{
    static void buildArray(int arr[], int n, int prefixArray[])
    {
        Arrays.fill(prefixArray, 0);
        prefixArray[n - 1] = arr[n - 1] * (int)(Math.pow(2, 0));
        for (int i = n - 2; i >= 0; i--)
        {
            prefixArray[i] = prefixArray[i + 1] + arr[i] * (1 << (n - 1 - i));
        }
    }
    
    static int getDeimalNum(int arr[], int left, int right, int n, int prefixArray[])
    {
        if (right != n - 1)
        {
            return (prefixArray[left] - prefixArray[right + 1]) / (1 << (n - 1 - right));
        }
        return prefixArray[left] / (1 << (n - 1 - right));
    }
    
    public static void main(String[] args)
    {
        int arr[] = {1, 0, 1, 1, 0, 0, 1, 1};
        int n = arr.length;

        int prefixArray[] = new int[n];
        buildArray(arr, n, prefixArray);

        System.out.println(getDeimalNum(arr,1, 5, n, prefixArray));

        System.out.println(getDeimalNum(arr,3, 6, n, prefixArray));
    }
}

12
9

Complexity Analysis for Queries for Decimal Values of Subarrays of a Binary Array

Time Complexity

O(q) where “q” is the number of queries.

Space Complexity

O(n) where “n” is the number of elements in the array.

Reference

Translate »