We have given an array of integer and a number of queries and we have to find out the number of all the distinct elements we have within the given range, the query consists of two numbers left and right, this is the given range, with this given range we have to find out the number of distinct elements.
Table of Contents
Example
Input:
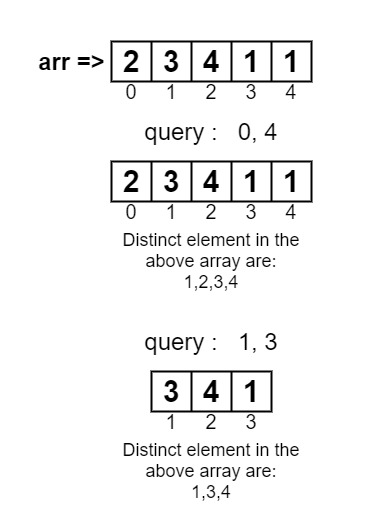
arr[] = {2,3,4,1,1}
0, 4
1, 3
2, 4
Output:
4 3 2
Explanation:
In the first query, the number of distinct integers in a[0…4] is 4 (4, 3, 2,1). In the second query, the number of distinct integers in a[1..3] is 3 (4, 3,1). In the third query, the number of distinct integers in a[2..4] is 2 (1, 4).
Algorithm
- Make the object array and with each position mark the values as left, right and the index associated with each object.
- Sort the query array with respect to the right value given as a range.
- Create an array binaryIndTree[].
- Start traversing the given array and simultaneously the given queries,
- check if the visitedArray [a[i]] is -1.
- If false, update the binaryIndTree array with value -1 at the index visitedArray [a[i]].
- Set visitedArray [a[i]] = i and update the binaryIndTree array binaryIndTree array with value 1 at index i.
- Set counter to 0, and start traverse till the counter is less than no of query and also till the queries right value is equal to i.
- For each queries’ index of the object, array update the value query index as the difference of the queries’ right value and the queries’ left value.
- Print all the results for each query defined.
Explanation
We are going to make an object array such that with that object array we are going to link the left, right and index or number of query. Then we are going to sort that query object such that the queries array sort in ascending order of ‘right’ values, means the query which has the least value of ‘right’ will comes first in order.
Now, create an array which is binaryIndTree. Initialize all the values of the array with 0, then create an array of size max, which is 1000001. Initialize all the values of this array to -1 and the last array of the output of size query, because there will the same number of output as the number of queries. The counter’s value should be set to 0. Now we start traversing the array and check if the visitedArray[arr[i]] = -1, if it is found to be true then update the value of binaryIndTree with value -1. After the update the value visitedArray[arr[i]] to i, and again update the binaryIndTree with the value 1, this is to be done whether the above condition is true or not.
Within this loop, start updating the array and this is to be done till the value of the counter is less than the value of the number of the query, q. Update the output array with the difference of queries’ right value and queries’ left value and update at each index, remember when we create the index as same as the number of queries. And increase the value of the counter. Finally, print all the values in the output array.
Implementation
C++ program for Queries for Number of Distinct Elements in a Subarray
#include<bits/stdc++.h>
using namespace std;
const int MAX = 1000001;
struct Query
{
int left, right, index;
};
bool compare(Query x, Query y)
{
return x.right < y.right;
}
void update(int index, int val, int binaryIndTree[], int n)
{
for (; index <= n; index += index&-index)
binaryIndTree[index] += val;
}
int query(int index, int binaryIndTree[], int n)
{
int sum = 0;
for (; index>0; index-=index&-index)
sum += binaryIndTree[index];
return sum;
}
void getQueryOutput(int arr[], int n, Query queries[], int q)
{
int binaryIndTree[n+1];
memset(binaryIndTree, 0, sizeof(binaryIndTree));
int visitedArray[MAX];
memset(visitedArray, -1, sizeof(visitedArray));
int output[q];
int counter = 0;
for (int i=0; i<n; i++)
{
if (visitedArray[arr[i]] !=-1)
update (visitedArray[arr[i]] + 1, -1, binaryIndTree, n);
visitedArray[arr[i]] = i;
update(i + 1, 1, binaryIndTree, n);
while (counter < q && queries[counter].right == i)
{
output[queries[counter].index] = query(queries[counter].right + 1, binaryIndTree, n)- query(queries[counter]. left, binaryIndTree, n);
counter++;
}
}
for (int i=0; i<q; i++)
cout << output[i] << endl;
}
int main()
{
int a[] = { 2,3,4,1,1};
int n = sizeof(a)/sizeof(a[0]);
Query queries[3];
queries[0].left = 0;
queries[0].right = 4;
queries[0].index = 0;
queries[1].left = 1;
queries[1].right = 3;
queries[1].index = 1;
queries[2].left = 2;
queries[2].right = 4;
queries[2].index = 2;
int q = sizeof(queries)/sizeof(queries[0]);
sort(queries, queries+q, compare);
getQueryOutput(a, n, queries, q);
return 0;
}
4 3 2
Java program for Queries for Number of Distinct Elements in a Subarray
import java.util.Arrays;
import java.util.Comparator;
class distinctElementsQuery
{
static int MAX = 1000001;
static class Query
{
int l, r, index;
}
static void update(int index, int val, int binaryIndTree[], int n)
{
for (; index <= n; index += index & -index)
binaryIndTree[index] += val;
}
static int query(int index, int binaryIndTree[], int n)
{
int sum = 0;
for (; index > 0; index -= index & -index)
sum += binaryIndTree[index];
return sum;
}
static void getQueryOutput(int[] arr, int n, Query[] queries, int q)
{
int[] binaryIndTree = new int[n + 1];
Arrays.fill(binaryIndTree, 0);
int[] visitedArray = new int[MAX];
Arrays.fill(visitedArray, -1);
int[] output = new int[q];
int counter = 0;
for (int i = 0; i < n; i++)
{
if (visitedArray[arr[i]] != -1)
update(visitedArray[arr[i]] + 1, -1, binaryIndTree, n);
visitedArray[arr[i]] = i;
update(i + 1, 1, binaryIndTree, n);
while (counter < q && queries[counter].r == i)
{
output[queries[counter].index] = query(queries[counter].r + 1, binaryIndTree, n) - query(queries[counter].l, binaryIndTree, n);
counter++;
}
}
for (int i = 0; i < q; i++)
System.out.println(output[i]);
}
public static void main(String[] args)
{
int a[] = { 2,3,4,1,1};
int n = a.length;
Query[] queries = new Query[3];
for (int i = 0; i < 3; i++)
queries[i] = new Query();
queries[0].l = 0;
queries[0].r = 4;
queries[0].index = 0;
queries[1].l = 1;
queries[1].r = 3;
queries[1].index = 1;
queries[2].l = 2;
queries[2].r = 4;
queries[2].index = 2;
int q = queries.length;
Arrays.sort(queries, new Comparator<Query>()
{
public int compare(Query x, Query y)
{
if (x.r < y.r)
return -1;
else if (x.r == y.r)
return 0;
else
return 1;
}
});
getQueryOutput(a, n, queries, q);
}
}
4 3 2
Complexity Analysis for Queries for Number of Distinct Elements in a Subarray
Time Complexity
O(queries * log n) where “n” is the size of the input array.
Space Complexity
O(n) where “n” is the number of elements in the array.