In the range minimum query problem we have given a query and an integer array. Each query contains the range as left and right indexes for each range. The given task is to determine the minimum of all number that lies within the range.
Table of Contents
Example
Input:
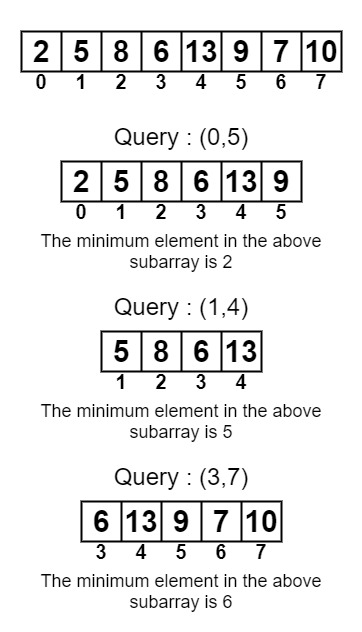
arr[] = {2, 5, 8, 6, 13, 9, 7, 10}
Query = {(0, 5), (1, 4), (3, 7)}
Output:
2 5 6
Explanation:
2 is the minimum among the range numbers {2, 5, 8, 6, 13, 9}
5 is the minimum among the range numbers {5, 8, 6, 13}
6 is the minimum among the range numbers {6, 13, 9, 7, 10}
Algorithm
- Create a 2D array and build it. For that, mark the 0th column of every row as its row index value.
- Traverse the array, and check if the array of lookup array at i, j-1 is less than the array of lookup array at i+2j-1, j-1, if true then update the lookup array at i, j as lookup array at i, j-1.
- Else update the lookup array at i, j as lookup array at i+2j-1, j-1
- For each given query, get the left and right range of the query, get the log value of right-left + 1 and check if the array of lookup at left, j is less than equal to the array of lookup at right – 2j +1, j, then return the value as an array of lookup at right – 2j + 1, j.
- Print the returned value
Explanation for Range Minimum Query (Square Root Decomposition and Sparse Table)
We have given an integer array and a range query, we have asked to find out the minimum value among all the integer values and return that value, for that we will be building the lookup array. The solution requires only the square root of n space but would consume sqrt(n) time, whereas for each given query, it will take the constant time but an extra space. The idea we will be putting forward in this is to determine all the possible minimum values in a subarray of size 2j where j can go up to log of n.
We will be building a lookup table, for that we will be using a lookup array. In the building of loop up the array, for each lookup at i, j hold a minimum of the values ranges from i to 2J. The lookup array at i, j will be holding the indexes of the values at each value of the array. While traversing through the array, we will determine the minimum value for any given range of possible size as 2 raised to the power j. Due to this, we will be able to find out the possible value at the given ranges.
For any given range query, we will be using ranges as in powers of 2. We will be using the range values to find the log of the difference of right-left + 1. Then we will compare the array of lookup at left, j is smaller than the array of right – 2j + 1, j, if the condition is found to be true, then return the value of the array at lookup at left, j, else return the array at lookup at right – 2j + 1, j. This will be the required answer.
Implementation
C++ program for Range Minimum Query (Square Root Decomposition and Sparse Table)
#include<iostream>
#include<math.h>
using namespace std;
#define MAX 500
int lookup[MAX][MAX];
struct Query
{
int Left, Right;
};
void buildLookup(int arr[], int n)
{
for (int i = 0; i < n; i++)
lookup[i][0] = i;
for (int j=1; (1<<j)<=n; j++)
{
for (int i=0; (i+(1<<j)-1) < n; i++)
{
if (arr[lookup[i][j-1]] < arr[lookup[i + (1<<(j-1))][j-1]])
lookup[i][j] = lookup[i][j-1];
else
lookup[i][j] = lookup[i + (1 << (j-1))][j-1];
}
}
}
int solveQuery(int arr[], int Left, int Right)
{
int j = (int)log2(Right - Left + 1);
if (arr[lookup[Left][j]] <= arr[lookup[Right - (1 << j) + 1][j]])
return arr[lookup[Left][j]];
else return arr[lookup[Right - (1<<j) + 1][j]];
}
void getMinimumNumber(int arr[], int n, Query q[], int m)
{
for (int i = 0; i < m; i++)
{
int Left = q[i].Left, Right = q[i].Right;
cout <<"Minimum value between ["<<Left<<", "<<Right<<"] is:"<< solveQuery(arr, Left, Right) << endl;
}
}
int main()
{
int a[] = {2,5,8,6,13,9,7,10};
int n = sizeof(a)/sizeof(a[0]);
Query q[] = {{0, 5}, {1, 4}, {3, 7}};
int m = sizeof(q)/sizeof(q[0]);
buildLookup(a, n);
getMinimumNumber(a, n, q, m);
return 0;
}
Minimum value between [0, 5] is:2 Minimum value between [1, 4] is:5 Minimum value between [3, 7] is:6
Java program for Range Minimum Query (Square Root Decomposition and Sparse Table)
class MinimumNumberQuery
{
static int MAX = 500;
static int [][]lookup = new int[MAX][MAX];
static class Query
{
int Left, Right;
public Query(int Left, int Right)
{
this.Left = Left;
this.Right = Right;
}
}
static void buildLookup(int arr[], int n)
{
for (int i = 0; i < n; i++)
lookup[i][0] = i;
for (int j = 1; (1 << j) <= n; j++)
{
for (int i = 0; (i + (1 << j) - 1) < n; i++)
{
if (arr[lookup[i][j - 1]] < arr[lookup[i + (1 << (j - 1))][j - 1]])
lookup[i][j] = lookup[i][j - 1];
else
lookup[i][j] = lookup[i + (1 << (j - 1))][j - 1];
}
}
}
static int solveQuery(int arr[], int Left, int Right)
{
int j = (int)Math.log(Right - Left + 1);
if (arr[lookup[Left][j]] <= arr[lookup[Right - (1 << j) + 1][j]])
return arr[lookup[Left][j]];
else return arr[lookup[Right - (1<<j) + 1][j]];
}
static void getMinimumNumber(int arr[], int n, Query q[], int m)
{
for (int i = 0; i < m; i++)
{
int Left = q[i].Left, Right = q[i].Right;
System.out.println("Minimum of [" + Left + ", " + Right +
"] is " + solveQuery(arr, Left, Right));
}
}
public static void main(String[] args)
{
int arr[] = {2,5,8,6,13,9,7,10};
int n = arr.length;
Query q[] = {new Query(0, 5),
new Query(1, 4),
new Query(3, 7)
};
int m = q.length;
buildLookup(arr, n);
getMinimumNumber(arr, n, q, m);
}
}
Minimum of [0, 5] is 2 Minimum of [1, 4] is 5 Minimum of [3, 7] is 6
Complexity Analysis for
Time Complexity
O(n Log n) where “n” is the number of elements in the array.
Space Complexity
O(n Log n) where “n” is the number of elements in the array.