Search in Sorted Rotated Array

Difficulty Level Medium
Frequently asked in Adobe Amazon Apple Bloomberg ByteDance eBay Expedia Facebook Goldman Sachs Google Microsoft Nvidia Oracle PayPal VMware Walmart Labs
Array Binary Search SortingViews 1821

An element search in sorted rotated array can be found using binary search in O(logn) time. The objective of this post is to find a given element in a sorted rotated array in O(logn) time. Some example of a sorted rotated array is given.

Example

Input  : arr[] = {7,8,9,10,1,2,3,5,6};
         key = 2
Output : Found at index 5

Input  : arr[] = {7,8,9,10,1,2,3,5,6};
         key = 30
Output : Not found

Input : arr[] = {4,8,16,1,2}
        key = 2   
Output : Found at index 4

Algorithm for Search in Sorted Rotated Array

  1. we first find the pivot element, a pivot element is an array element in a sorted rotated array whose both the neighbors (in the array) are less than it. Basically, the pivot is the largest element in an array. pivotSearch() returns the index of pivot.
  2. Once the pivot has been found, we perform a binary search range[0,p] or range[p,n-1] depending upon the value of the element to be searched.

here,

p = index of pivot

n = size of the array

arr[] = {7,8,9,10,1,2,3,5,6}
Element to Search = 2
  1.find out pivot p and divide the array into two subarrays range[lo,p] and range[p,hi]
  2.perform binary search in one of the subarrays.
      a. if key >= arr[0], call binary search in range[lo,p].
      b. else call binary search in range[p,hi]
  3.if key is found in selected sub-array then return it's index 
       else return -1.

lo(index number of first array element) = 0
hi(index number of last array element) = n-1
p = index of pivot
n = size of the array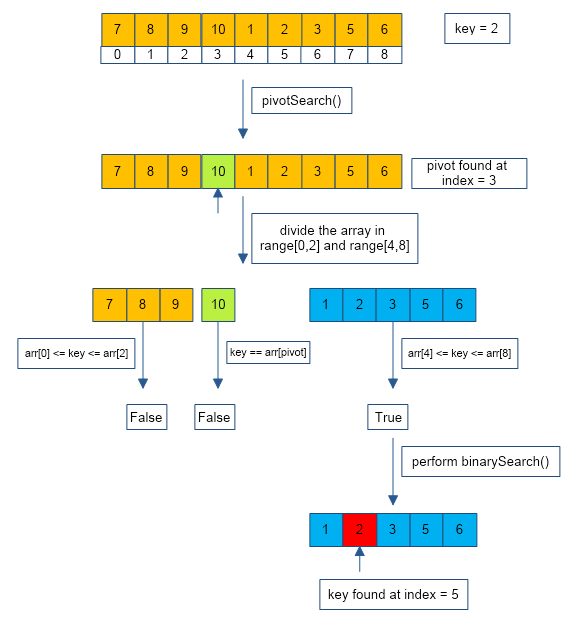

Search in Sorted Rotated Array

Implementation

C++ Program

#include <bits/stdc++.h> 
using namespace std; 

// Standard Binary Search function
int binarySearch(int arr[],int lo,int hi,int key) 
{ 
    if (lo <= hi)
    {
        int mid = (lo+hi)/2; /*low + (high - low)/2;*/
        
        if (key == arr[mid]) 
        	return mid; 
        	
        if (key > arr[mid]) 
        	return binarySearch(arr,mid+1,hi,key);
        	
        else
        	return binarySearch(arr,lo,mid-1,key); 
    }
    
    return -1;  // low > high
} 

/* Function to get pivot. For sorted rotated array 7,9,11,12,1,3 it returns 3 (index of 12) */
int pivotSearch(int arr[],int lo,int hi) 
{ 
    // base cases
    if (hi < lo) 
    return -1;      // if array is not rotated at all
    if (hi == lo) 
    return lo; 
    
    int mid = (lo+hi)/2; /*lo + (hi-lo)/2;*/
    
    // pivot is greater than array element to it's right
    if (mid < hi && arr[mid] > arr[mid+1]) 
    	return mid; 
    // pivot is greater than array element to it's left
    if (mid > lo && arr[mid] < arr[mid-1]) 
    	return (mid-1); 
    	
    
    if (arr[lo] >= arr[mid]) 
    	return pivotSearch(arr,lo,mid-1);   // pivot lies in left half 
    else
        return pivotSearch(arr,mid+1,hi);   // pivot lies in right half
    
} 

int pivotedBinarySearch(int arr[],int n,int key) 
{ 
    int pivot = pivotSearch(arr,0,n-1); // obtain the pivot index 
    
    // If no pivot is found,then array is not rotated at all 
    // in this case we perform a simple binary search as array is sorted (but not rotated)
    if (pivot == -1) 
    	return binarySearch(arr,0,n-1,key); 
    
    // If we found a pivot, then first compare with pivot value 
    if (arr[pivot] == key) 
    	return pivot; 
    
    // else perform binary search in two subarrays around pivot 
    
    // if element to be searched is greater than first (0-index) array element
    // then searched element lies between indices - 0 and pivot
    if (arr[0] <= key) 
    	return binarySearch(arr,0,pivot-1,key);
    // else it lies between indices - pivot and n-1
    else	
    	return binarySearch(arr,pivot+1,n-1,key);
} 

/* Main program to implement above functions */
int main() 
{ 
    // element to be searched = 3 
    int arr[] = {7,8,9,10,1,2,3,5,6}; 
    int n = sizeof(arr)/sizeof(arr[0]); 
    int search = 2; 
    	
    cout << "Index of "<<search<<" : "<<pivotedBinarySearch(arr,n,search); 
    			
    return 0; 
} 

Index of 2 : 5

Java Program

class sortedRotatedSearch 
{ 
    // Standard Binary Search function
    static int binarySearch(int arr[],int lo,int hi,int key) 
    { 
        if (lo <= hi)
        {
            int mid = (lo+hi)/2; /*low + (high - low)/2;*/
            
            if (key == arr[mid]) 
            	return mid; 
            	
            if (key > arr[mid]) 
            	return binarySearch(arr,mid+1,hi,key);
            	
            else
            	return binarySearch(arr,lo,mid-1,key); 
        }
        
        return -1;  // low > high
    } 
    
    /* Function to get pivot. For sorted rotated array 7,9,11,12,1,3 it returns 3 (index of 12) */
    static int pivotSearch(int arr[],int lo,int hi) 
    { 
        // base cases
        if (hi < lo) 
        return -1;      // if array is not rotated at all
        if (hi == lo) 
        return lo; 
        
        int mid = (lo+hi)/2; /*lo + (hi-lo)/2;*/
        
        // pivot is greater than array element to it's right
        if (mid < hi && arr[mid] > arr[mid+1]) 
        	return mid; 
        // pivot is greater than array element to it's left
        if (mid > lo && arr[mid] < arr[mid-1]) 
        	return (mid-1); 
        	
        
        if (arr[lo] >= arr[mid]) 
        	return pivotSearch(arr,lo,mid-1);   // pivot lies in left half 
        else
            return pivotSearch(arr,mid+1,hi);   // pivot lies in right half
        
    } 
    
    // function to search an element in sorted-rotated array
    static int pivotedBinarySearch(int arr[],int n,int key) 
    { 
        int pivot = pivotSearch(arr,0,n-1); // obtain the pivot index 
        
        // If no pivot is found,then array is not rotated at all 
        // in this case we perform a simple binary search as array is sorted (but not rotated)
        if (pivot == -1) 
        	return binarySearch(arr,0,n-1,key); 
        
        // If we found a pivot, then first compare with pivot value 
        if (arr[pivot] == key) 
        	return pivot; 
        
        // else perform binary search in two subarrays around pivot 
        
        // if element to be searched is greater than first (0-index) array element
        // then searched element lies between indices - 0 and pivot
        if (arr[0] <= key) 
        	return binarySearch(arr,0,pivot-1,key);
        // else it lies between indices - pivot and n-1
        else	
        	return binarySearch(arr,pivot+1,n-1,key);
    } 
    
    // main function to implement above function 
    public static void main(String args[]) 
    { 
       // Let us search 3 in below array 
       int arr[] = {7,8,9,10,1,2,3,5,6};
       int n = arr.length; 
       int key = 2; 
       System.out.println("Index of "+key+" is : "+ pivotedBinarySearch(arr,n,key)); 
    } 
}
Index of 2 is : 5

Improvised Solution/Algorithm for Search in Sorted Rotated Array

we can search an element in the sorted-rotated array in a single pass of binary search. The idea is to look for a particular range of sorted array elements in which the searched element can lie. Once such a range is found, we perform a binary search in that range to look for the searched element. Below is the process :

assume ‘key’ is the element to be searched.

1. find mid point of the range [lo,hi] as mid = (lo+hi)/2
2. if arr[mid] == key : return mid.
3. else if range [lo,mid-1] is sorted
    a. if arr[lo] <= key <= arr[mid],search for key in range[lo,mid].
    b. else recur for range [mid+1,hi].
4. else range[mid+1,hi] must be sorted
    a. if arr[mid+1] <= search <= arr[hi],search for key range[mid+1,hi].
    b. else recur for range [lo,mid].

The following are C++ and Java Implementations of the above algorithm.

Implementation

C++ Program

#include <bits/stdc++.h> 
using namespace std; 

// Returns index of searched element 'key' in arr[lo,hi] if key is present 
// or else returns -1 
int find(int arr[],int lo,int hi,int key) 
{ 
  if (lo > hi) 
  return -1; 

  int mid = (lo+hi)/2; 
  
  if (arr[mid] == key) 
  return mid; 

  // if arr[lo,mid-1] is sorted
  if (arr[lo] <= arr[mid]) 
  {
    if (key >= arr[lo] && key <= arr[mid]) 
    return find(arr,lo,mid-1,key);      // check if key lies in range[lo,mid-1]
    
    else
    return find(arr,mid+1,hi,key);      // else recur for range[mid+1,hi]
  } 
    // else arr[mid+1,hi] must be sorted
    else
    {
    	if (key >= arr[mid] && key <= arr[hi]) 
    	return find(arr,mid+1,hi,key);         // check if key lies in range[mid+1,hi]
        
        else
    	return find(arr,lo,mid-1,key);         // else recur for range[lo,mid-1]
    }
} 

// Main Program to implement above functions
int main() 
{ 
  int arr[] = {7,8,9,10,1,2,3,5,6};
  int n = sizeof(arr)/sizeof(arr[0]); 
  int key = 2; 
  int i = find(arr, 0, n-1, key); 

  i != -1 ? cout<<"Index of "<<key<<" : "<<i<<endl : cout<<"Element Not found";
} 

Index of 2 : 5

Java Program

class sortedRotatedSearch 
{ 
    // Returns index of searched element 'key' in arr[lo,hi] if key is present 
    // or else returns -1 
    static int find(int arr[],int lo,int hi,int key) 
    { 
    	if (lo > hi) 
    	return -1; 
    
    	int mid = (lo+hi)/2; 
    	
    	if (arr[mid] == key) 
    	return mid; 
    
    	// if arr[lo,mid-1] is sorted
    	if (arr[lo] <= arr[mid]) 
    	{
    		if (key >= arr[lo] && key <= arr[mid]) 
    		return find(arr,lo,mid-1,key);      // check if key lies in range[lo,mid-1]
    		
    		else
    		return find(arr,mid+1,hi,key);      // else recur for range[mid+1,hi]
    	} 
        // else arr[mid+1,hi] must be sorted
        else
        {
        	if (key >= arr[mid] && key <= arr[hi]) 
        	return find(arr,mid+1,hi,key);         // check if key lies in range[mid+1,hi]
            
            else
        	return find(arr,lo,mid-1,key);         // else recur for range[lo,mid-1]
        }
    } 

    // Main Program to implement above functions
    public static void main(String args[]) 
    { 
    	int arr[] = {7,8,9,10,1,2,3,5,6};
    	int n = arr.length; 
    	int key = 2; 
    	int i = find(arr,0,n-1,key); 
    
    	if (i != -1)  
            System.out.println("Index of "+key+" : "+i); 
        else
            System.out.println("Key not found"); 
    } 
} 

Index of 2 : 5

Complexity Analysis

  1. Time Complexity T(n) = O(logn)
  2. Space Complexity A(n) = O(1)

Supplementary Information :

  • The above algorithm does not apply when the sorted rotated array contains duplicate elements.

References

Translate ยป