Binary array after M range toggle operations

You are given a binary array, which consists of 0 initially and Q number of queries. The problem statement asks to toggle the values (converting 0s into 1s and 1s into 0s). After the Q queries performed, print the resultant array.

Example

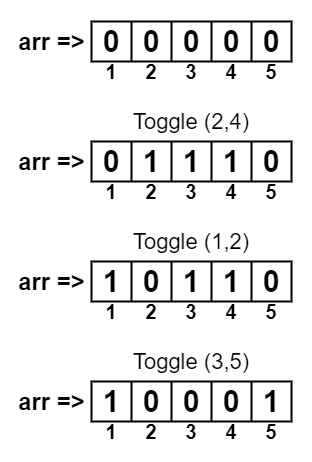
arr[] = {0, 0, 0, 0, 0}

Toggle(2,4)

Toggle(1,2)

Toggle(3,5)

1 0 0 0 1

Explanation

1st toggling  ⇒ 0,1,1,1,0

2nd toggling ⇒ 1,0,1,1,0

3rd toggling ⇒ 1,0,0,0,1

Algorithm

1. Create an n+2 sized Boolean array.
2. Initialize the boolean array as false for each index.
3. Now for each query flip the element at index left and right + 1.
4. Now simply fill the array as prefix xor array. Store the xor of all the elements from index 1 to i at index i.
5. Print the array

Explanation for Binary array after M range toggle operations

Given a binary array, which consists of 0s and 1s and as the name suggests. But initially, it only contains the values as 0s. Given the Q number of queries. Each query contains two values, the values are the starting point of a range and an ending point of a range, within these ranges, we have to toggle the values where toggling means we have to convert 0s into 1s and 1s into 0s Q number (query number) of times. For this, we are going to create a Boolean array, of size two more the length of the array n+2. Then we are going to toggling the values Q number of times, if we have more number of queries, we do not have to call it by our self, instead, we will make a loop and call it with different query number and inputs.

In the toggling convert the values at the exact places given as a range in the same array,  convert all the zeroes into the ones, and ones it to zero by performing the XOR operation. XOR operation does the same for us if it is found the same numbers or values it will give the 0 as result means false if it finds a different number of values. It will give the 1, as a result, means true. So we will do the same in the toggling function to invert values.

Traverse the array, and perform the operation on the array. Perform the XOR operation on the current and the previous value of the array. The thing we did as if it finds the same bit it will give 0 otherwise 1. This operation will be the last to toggle all the values which will become within a range. Finally, print the array.

Code

Implementation in C++ for Binary array after M range toggle operations

#include<iostream>

using namespace std;

void Toggle(bool arr[], int start, int end)
{
    arr[start] ^= 1;
    arr[end+1] ^= 1;
}

void getToggling(bool arr[], int n)
{
    for (int k=1; k<=n; k++)
        arr[k] ^= arr[k-1];
}

void printOutput(bool arr[], int n)
{
    for (int k=1; k<=n; k++)
        cout << arr[k] <<" ";
}

int main()
{
    int n = 5, m = 3;
    bool arr[n+2] = {0};

    Toggle(arr, 1, 5);
    Toggle(arr, 2, 5);
    Toggle(arr, 3, 5);

    getToggling(arr, n);

    printOutput(arr, n);
    return 0;
}

1 0 1 1 1

Implementation in Java for Binary array after M range toggle operations

class ToggleArray
{
    static void Toggle(boolean arr[], int start, int end)
    {
        arr[start] ^= true;
        arr[end + 1] ^= true;
    }

    static void getToggling(boolean arr[], int n)
    {
        for (int k = 1; k <= n; k++)
        {
            arr[k] ^= arr[k - 1];
        }
    }

    static void printOutput(boolean arr[], int n)
    {
        for (int k = 1; k <= n; k++)
        {
            if(arr[k] == true)
                System.out.print("1" + " ");
            else
                System.out.print("0" + " ");
        }
    }

    public static void main(String args[])
    {
        int n = 5, m = 3;
        boolean arr[] = new boolean[n + 2];

        Toggle(arr, 1, 5);
        Toggle(arr, 2, 5);
        Toggle(arr, 3, 5);

        getToggling(arr, n);

        printOutput(arr, n);
    }
}

1 0 1 1 1

Complexity Analysis

Time Complexity

O(n+q) where “n” is the number of elements in the array and “q” is the number of queries. All the queries are being performed in O(1) time and then updation requires O(N) time.

Space Complexity

O(n) where “n” is the number of elements in the array.