Friends Pairing Problem

Difficulty Level Easy
Frequently asked in Amazon Expedia GE Healthcare Google Honeywell JP Morgan
Dynamic Programming Modular ArithmeticViews 2127

Problem Statement

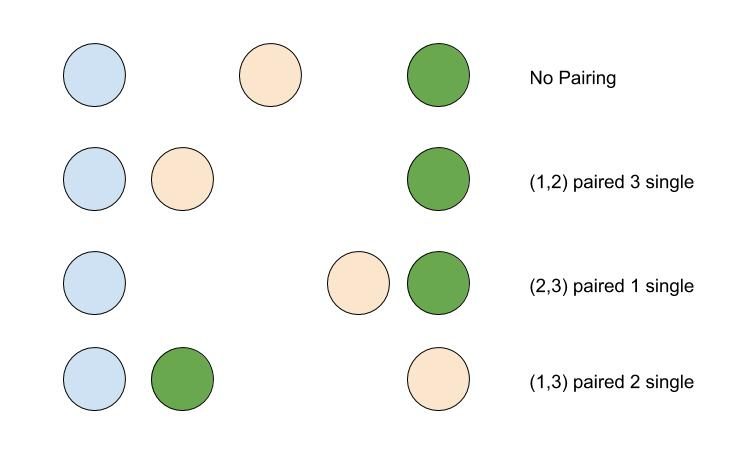
The “Friends Pairing Problem” states that there are N friends. And each them can remain single or be paired up with each other. But once a pair is made, those two friends can not take part in pairing. So, you need to find the total number of ways in which friends can be paired up or they can remain single.A

Example

3
4

Friends Pairing Problem
Approach for Friends Pairing Problem

Instead of thinking about it as a big problem. Let’s first try to solve for smaller N. For N = 1, the answer is 1. For N = 2, the answer is 2. Either both the friends remain single or they pair up. For N = 3, either the third friend can stay single. So for that answer should be answer to the problem with N = 2. Cause in all those cases our third friend can stay single. And for pairing, it can choose any one of the friends. So choosing 1 friend from N-1 friends and then number of ways in which others can pair/stay single = (N-1)*F(N-2). Now, we can think of the recursive formula for the problem.

F(N)     =     F(N-1)   +   (N-1)*F(N-2)
                  ^              ^
                  |              |
Nth friend (stays single) (pairs with N-1 friends)

From the recursive formula, we can see that while computing F(N) we calculate F(N-2). And then for F(N-1) as well, we compute F(N-2). So instead of recomputing values, we should use dynamic programming. Here, we can store the whole F(N) values from 0 to N. But that is not required. Since the value of F(N) is only dependent on F(N-1) and F(N-2) that is last 2 values. So we will just keep on storing last 2 values. Cause that will save us space.

Code

C++ code for Friends Pairing Problem

#include<bits/stdc++.h>
using namespace std;

int main()
{
  // number of friends
  int n;cin>>n;

  int last = 2, lastTolast = 1;
  // here last denotes F(N-1) and lastTolast denotes F(N-2)
  // we can also use a dp array but that will only increase space complexity
  // and from the recursive formula we can see that
  // F(N) is dependent only on F(N-1) and F(N-2)
  int current;
  for(int i=3;i<=n;i++){
    current = last + (i-1)*lastTolast;
    lastTolast = last;
    last = current;
  }
  cout<<current<<endl;
}E

4
10

Java code for Friends Pairing Problem

import java.util.*;

class Main{
  
  public static void main(String[] args)
  {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();// number of friends

    int last = 2, lastTolast = 1;
    // here last denotes F(N-1) and lastTolast denotes F(N-2)
    // we can also use a dp array but that will only increase space complexity
    // and from the recursive formula we can see that
    // F(N) is dependent only on F(N-1) and F(N-2)
    int current;
    for(int i=3;i<=n;i++){
      current = last + (i-1)*lastTolast;
      lastTolast = last;
      last = current;
    }
    System.out.println(current);
  }
}
4
10

Complexity Analysis

Time Complexity

O(N), because we have to run a loop until N to find it. Since F(N) is dependent on F(N-1) and F(N-2).

Space Complexity

O(1), we used only three variables for computation and thus the spaced required was constant.

Translate ยป