K maximum sums of overlapping contiguous sub-arrays

Difficulty Level Hard
Frequently asked in CodeNation Dell Facebook GE Healthcare Google Qualcomm
Array Dynamic ProgrammingViews 2377

Problem Statement

The problem “K maximum sums of overlapping contiguous sub-arrays” states that you are given an array of integers. Find the maximum sum of k-subarrays such that their sum is maximum. These k-subarrays might be overlapping. So, we need to find k-subarrays such that their sum is maximum among other subarrays.

Example

K maximum sums of overlapping contiguous sub-arrays

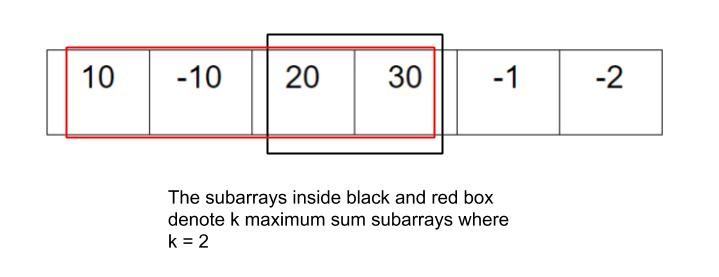
arr = {10,-10,20,30,-1,-2}, k = 2
50 50

Explanation: The subarray having sum = 50 has the maximum value. After that, if we in the left or in the right direction the sum is decreased. So, if we move in the left direction. We can again get a sum of 50 because -10 and 10 cancel each other. But if we move in the right direction, our sum will only keep on decreasing. So, this is the best possible answer we could get.

arr = {-1,-2,-3,-4}, k = 3
-1 -2 -3

Explanation: Here if we combine any of the two numbers, that will result in a worse solution. So, choosing a single number will be better. Thus, we will choose single numbers -1 -2 -3. Any other combination will give us a worse result.

Approach for K maximum sums of overlapping contiguous sub-arrays

The problem asks us to find the k maximum sums among all the sums of all the subarray. So, if we think of using Kadane’s algorithm. We won’t be able to solve the problem. Because Kadane’s algorithm can be used to find the maximum sum. But that won’t be able to find the second maximum, third maximum and others. Kadane’s algorithm mainly focuses on finding the first maximum and does not aim to find the next maximum subarray sum. Here we create two arrays of minimumKSum and maximumKSum. We will use a prefix sum array to find the sum of subarrays for the current index. Array minimumKSum keeps the k minimum sum of subarrays. Array maximumKSum keeps the k maximum sum of subarrays. Now for each index, we update the minimumKSum and maximumKSum arrays. After traversing through the array, answer is stored inside maximumKSum.

Code

C++ code to find K maximum sums of overlapping contiguous sub-array

#include<bits/stdc++.h>
using namespace std;

void kMaxSubArrays(vector<int> input, int k)
{
  int n = input.size();
  vector<int> prefixSum(n);
    prefixSum[0] = input[0];
    for(int i=1;i<n;i++)
        prefixSum[i] += prefixSum[i-1] + input[i];

  vector<int> minimumKSum(k, INT_MAX);
  minimumKSum[0] = 0;

  vector<int> maximumKSum(k, INT_MIN);
  vector<int> currentSum(k);

  for (int i = 0; i < n; i++) {
    for (int j = 0; j < k; j++) {
      if(prefixSum[i] < 0 && minimumKSum[j]==INT_MAX)
            currentSum[j]=(-prefixSum[i])-minimumKSum[j];
        else
                currentSum[j] = prefixSum[i] - minimumKSum[j];
    }
        int j = 0;
        for (int l = 0; l < k; l++) {
            if (currentSum[j] > maximumKSum[l]) {
                maximumKSum.insert(maximumKSum.begin() + l, currentSum[j]);
                maximumKSum.erase(maximumKSum.begin() + k);
                j++;
            }
        }
    for (int j = 0; j < k; j++) {
            if (prefixSum[i] < minimumKSum[j]) {
                minimumKSum.insert(minimumKSum.begin() + j, prefixSum[i]);
                minimumKSum.erase(minimumKSum.begin() + k);
                break;
            }
        }
  }

  for (int element : maximumKSum)
    cout<<element<<" ";
}

int main()
{
  int inputSize;cin>>inputSize;
  vector<int> input(inputSize);
  for(int i=0;i<inputSize;i++)cin>>input[i];
  int k;cin>>k;
  kMaxSubArrays(input, k);
}

6
10 -10 20 30 -1 -2
2
50 50

Java code to find K maximum sums of overlapping contiguous sub-array

import java.util.*;

class Main{
    
    static void kMaxSubArrays(int input[], int k)
    {
    	int n = input.length;
    	int prefixSum[] = new int[n];
        prefixSum[0] = input[0];
        for(int i=1;i<n;i++)
            prefixSum[i] += prefixSum[i-1] + input[i];
    
    	int maximumKSum[] = new int[k];
    	for(int i=0;i<k;i++)
    	    maximumKSum[i] = Integer.MIN_VALUE;
    
    	int minimumKSum[] = new int[k];
    	for(int i=0;i<k;i++)
    	    minimumKSum[i] = Integer.MAX_VALUE;
    	minimumKSum[0] = 0;
    	
    	int currentSum[] = new int[k];
    	for(int i=0;i<k;i++)
    	    currentSum[i] = 0;
    
    	for (int i=0;i<n;i++) {
    		for (int j=0;j<k;j++) {
    			if(prefixSum[i] < 0 && minimumKSum[j]==Integer.MAX_VALUE)
    		        currentSum[j]=(-prefixSum[i])-minimumKSum[j];
    		    else
                    currentSum[j] = prefixSum[i] - minimumKSum[j];
    		}
            int j = 0;
            for (int l = 0; l < k; l++) {
                if (currentSum[j] > maximumKSum[l]) {
                    maximumKSum[l] = currentSum[j];
                    for(int z = l+1;z<k;z++)
                        maximumKSum[z] = maximumKSum[z-1];
                    j++;
                }
            }
    		for (j = 0; j < k; j++) {
                if (prefixSum[i] < minimumKSum[j]) {
                    minimumKSum[j] = prefixSum[i];
                    for(int z = j+1;z<k;z++)
                        minimumKSum[z] = minimumKSum[z-1];
                    break;
                }
            }
    	}
    
    	for(int i=0;i<k;i++)
    		System.out.print(maximumKSum[i]+" ");
    }
    
    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
    	int inputSize = sc.nextInt();
    	int input[] = new int[inputSize];
    	for(int i=0;i<inputSize;i++)input[i] = sc.nextInt();
    	int k = sc.nextInt();
    	kMaxSubArrays(input, k);
    }
}

6
10 -10 20 30 -1 -2
2
50 50

Complexity analysis

Time Complexity: O(k*N)

Insertion in minimumKSum and insertion in maximumKSum take O(k) time. And we are doing this process inside a loop that is looping over each element of the array. Hence, the overall time complexity is O(k*n).

Space Complexity: O(N)

We are storing the input in inputArray which marks the upper bound for space. Thus space complexity of the solution is linear.

Translate ยป